题目内容
16. 如图,在平面直角坐标系中有一个△ABC,点A(-1,3),B(2,0),C(-3,-1).
如图,在平面直角坐标系中有一个△ABC,点A(-1,3),B(2,0),C(-3,-1).(1)画出△ABC关于y轴的对称轴图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为2,则△ABC的面积是多少?写出解答过程.
分析 (1)作出各点关于y轴的对称点,再顺次连接即可;
(2)利用矩形的面积减去各顶点上三角形的面积即可.
解答  解:(1)如图;
解:(1)如图;
(2)∵网格上的每个小正方形的边长为2,
∴S△ABC=8×10-$\frac{1}{2}$×4×8-$\frac{1}{2}$×6×6-$\frac{1}{2}$×2×10
=80-16-18-10=36.
答:△ABC的面积是36.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
7.若抛物线y=x2-x-1与x轴的交点坐标为(m,0),则代数式m2-m+2012的值为( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
8.下列有理数大小关系判断正确的是( )
| A. | 0>|-10| | B. | -(-$\frac{1}{9}$)>-|-$\frac{1}{10}$| | C. | |-3|<|+3| | D. | -1>-0.01 |
6.y=$\frac{6}{x}$上有两点A(x1,y1)与B(x2,y2),若x1<x2,则y1与y2的关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
 如图,在△ABC中,点D在边AB上,AD=20cm,BD=16cm,BC=24cm,点E在边AC上,且△ADE与△BCD相似.
如图,在△ABC中,点D在边AB上,AD=20cm,BD=16cm,BC=24cm,点E在边AC上,且△ADE与△BCD相似. 如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=35°,则∠BAD=55°.
如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=35°,则∠BAD=55°.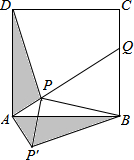 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 如图,已知△ABC≌△ABD,∠CAB=30°,∠D=40°,则∠CBE=70°.
如图,已知△ABC≌△ABD,∠CAB=30°,∠D=40°,则∠CBE=70°.