题目内容
1.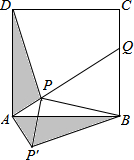 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
分析 (1)根据正方形的性质得AB=AD,∠BAD=90°,再利用旋转的性质得AP=AP′,∠PAP′=∠DAB=90°,于是可判断△APP′是等腰直角三角形;
(2)根据等腰直角三角形的性质得PP′=$\sqrt{2}$PA=$\sqrt{2}$,∠APP′=45°,再利用旋转的性质得PD=P′B=$\sqrt{10}$,接着根据勾股定理的逆定理可证明△PP′B为直角三角形,∠P′PB=90°,然后利用平角定义计算∠BPQ的度数.
解答 (1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形;
(2)解:∵△APP′是等腰直角三角形,
∴PP′=$\sqrt{2}$PA=$\sqrt{2}$,∠APP′=45°,
∵△ADP沿点A旋转至△ABP′,
∴PD=P′B=$\sqrt{10}$,
在△PP′B中,PP′=$\sqrt{2}$,PB=2$\sqrt{2}$,P′B=$\sqrt{10}$,
∵($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°-∠APP′-∠P′PB=180°-45°-90°=45°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质和勾股定理的逆定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.对于二次函数y=(x-2)2+2的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 对称轴是x=-2 | C. | 顶点坐标是(-2,2) | D. | 与x轴无交点 |

 如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm.
如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm. 如图,在平面直角坐标系中有一个△ABC,点A(-1,3),B(2,0),C(-3,-1).
如图,在平面直角坐标系中有一个△ABC,点A(-1,3),B(2,0),C(-3,-1).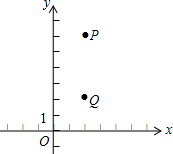 在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.
在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点. 如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2$\sqrt{3}$cm,E为AB的中点,P为AD上一点,PE+PB的最小值为2$\sqrt{3}$.
如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2$\sqrt{3}$cm,E为AB的中点,P为AD上一点,PE+PB的最小值为2$\sqrt{3}$.