题目内容
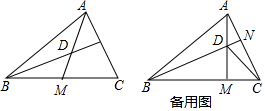
3.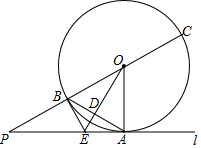 如图,直线1与⊙O相切于点A,点P在直线1上,直线PO交⊙O于点B、C,OD⊥AB,垂足为D,交PA于点E.
如图,直线1与⊙O相切于点A,点P在直线1上,直线PO交⊙O于点B、C,OD⊥AB,垂足为D,交PA于点E.(1)判断直线BE与⊙O的位置关系,并说明理由;
(2)若PB=OB=6,求$\widehat{AC}$的长.
分析 (1)利用SAS证明△AOE≌△BOE可得:∠EBO=∠EAO=90°,所以直线BE与⊙O相切;
(2)根据直角三角形斜边中线等于斜边一半可得:AB=6,可得△AOB是等边三角形,再求$\widehat{AC}$的圆心角,代入弧长公式得结论.
解答 解:(1)直线BE与⊙O相切,
理由是:∵OB=OA,OD⊥AB,
∴∠AOD=∠BOD,
∵直线1与⊙O相切于点A,
∴∠EAO=90°,
在△AOE和△BOE中,
∵$\left\{\begin{array}{l}{OA=OB}\\{∠AOD=∠BOD}\\{OE=OE}\end{array}\right.$,
∴△AOE≌△BOE(SAS),
∴∠EBO=∠EAO=90°,
∴直线BE与⊙O相切;
(2)在Rt△PAO中,
∵PB=OB=6,
∴AB=$\frac{1}{2}$OP=OB=6
∴AB=OB=OA
∴△AOB是等边三角形
∴∠AOB=60°
∴∠AOC=120°
∴${l}_{\widehat{AC}}$=$\frac{120π×60}{180}$=40π.
点评 本题考查了直角三角形斜边的中线的性质、三角形全等的性质和判定、弧长公式、切线的性质和判定,熟练掌握切线的判定方法和弧长公式是关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.|(-3)-5|等于( )
| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
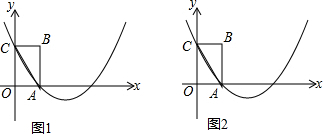
15.已知抛物线L:y=ax2+bx+c与抛物线L′:y=x2-2mx+4m+1关于直线x=2对称,且L′交y轴于点P(0,21),则方程ax2+bx+c=0的两个根为( )
| A. | x1=0,x2=3 | B. | x1=1,x2=-3 | C. | x1=3,x2=7 | D. | x1=-7,x2=-3 |

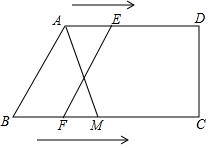 在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,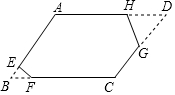 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )