题目内容
1. 如图,Rt△ABC中,∠ACB=90°,半径长为1的圆A与边AB交于点D、与边AC交于点E,联结DE并延长,与线段BC的延长线交于点P.
如图,Rt△ABC中,∠ACB=90°,半径长为1的圆A与边AB交于点D、与边AC交于点E,联结DE并延长,与线段BC的延长线交于点P.(1)若CE=2,BD=BC,求AB的值;
(2)过点D作DH⊥AC,若$\frac{EH}{DH}$=$\frac{1}{3}$,且CE=2,BP=5,求△BPD的面积.
分析 (1)设BD=BC=x,得出AB=1+x、AC=3,根据AB2=BC2+AC2可得(1+x)2=x2+32可得答案;
(2)设EH=a,则DH=3a,Rt△DEH中根据勾股定理求得EH=$\frac{1}{5}$,从而得CH=$\frac{11}{5}$,作DG⊥BP得DG=CH=$\frac{11}{5}$,根据三角形面积公式可得答案.
解答 解:(1)设BD=BC=x,
∵AD=AE=1,CE=2,
∴AB=1+x,AC=AE+CE=3,
由AB2=BC2+AC2可得(1+x)2=x2+32,
解得:x=4,
∴AB=5;
(2)设EH=a,则DH=3a,
∴AH=1-a,
∵DH⊥AC,
∴AD2=AH2+DH2,即1=(1-a)2+(3a)2,
解得:a=0(舍)或a=$\frac{1}{5}$,即EH=$\frac{1}{5}$,
∵CE=2,
∴CH=CE+EH=2+$\frac{1}{5}$=$\frac{11}{5}$,
过点D作DG⊥BP于点G,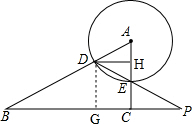
∴四边形CHDG为矩形,
∴DG=CH=$\frac{11}{5}$,
则S△BDP=$\frac{1}{2}$×BP×DG=$\frac{1}{2}$×5×$\frac{11}{5}$=$\frac{11}{2}$.
点评 本题主要考查勾股定理和矩形的判定与性质及三角形的面积,熟练掌握勾股定理求得所需线段的长是解题的关键.

练习册系列答案
相关题目
2.如果m表示有理数,那么|m|-m的值( )
| A. | 不可能是负数 | B. | 可能是零或者负数 | ||
| C. | 必定是零 | D. | 必定是正数 |
13.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解的范围是( )
| x | 6.17 | 6.18 | 6.19 |
| y | -0.03 | -0.01 | 0.02 |
| A. | -0.03<x<-0.01 | B. | -0.01<x<0.02 | C. | 6.18<x<6.19 | D. | 6.17<x<6.18 |
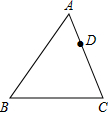 如图,在△ABC中,AB=8,AC=6,点D在AC上,AD=2,若点E在AB上,以A,D,E为顶点的三角形与△ABC相似.求AE的长.
如图,在△ABC中,AB=8,AC=6,点D在AC上,AD=2,若点E在AB上,以A,D,E为顶点的三角形与△ABC相似.求AE的长.