题目内容
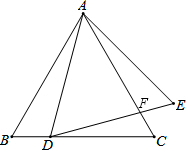 如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
考点:相似三角形的判定
专题:
分析:(1)利用等边三角形的性质以及相似三角形的判定方法两角对应相等的两三角形相似得出即可;
(2)利用对顶角的性质以及相似三角形的性质进而判断得出即可.
(2)利用对顶角的性质以及相似三角形的性质进而判断得出即可.
解答: (1)证明:∵△ABC,△ADE为等边三角形,
(1)证明:∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,
∴△AEF∽△DCF,
∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
 (1)证明:∵△ABC,△ADE为等边三角形,
(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,
∴△AEF∽△DCF,
∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
点评:此题主要考查了相似三角形的判定方法以及等边三角形的性质等知识,得出对应角关系是解题关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
说明命题“如果a,b,c是△ABC的三边,那么长为a-1,b-1,c-1的三条线段能构成三角形”是假命题的反例可以是( )
| A、a=2,b=2,c=3 |
| B、a=2,b=2,c=2 |
| C、a=3,b=3,c=4 |
| D、a=3,b=4,c=5 |
 如图,在平面直角坐标系xOy中,矩形ABCD的边AD=6,A(1,0),B(9,0),直线y=kx+b经过B、D两点.
如图,在平面直角坐标系xOy中,矩形ABCD的边AD=6,A(1,0),B(9,0),直线y=kx+b经过B、D两点.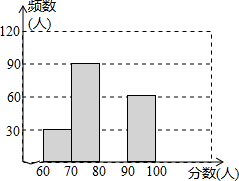 为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表.
为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表. 如图,小亮为了测出旗杆CD的高度,在平地上选择一点A,用测角仪测得旗杆顶端D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上),用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.求旗杆高CD(结果用根号表示).
如图,小亮为了测出旗杆CD的高度,在平地上选择一点A,用测角仪测得旗杆顶端D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上),用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.求旗杆高CD(结果用根号表示).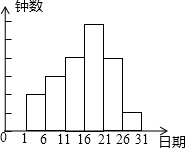 在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
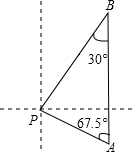 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1) 如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC:OA=1:2,且量得CD=12mm,则零件的厚度x=
如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC:OA=1:2,且量得CD=12mm,则零件的厚度x=