题目内容
 如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC:OA=1:2,且量得CD=12mm,则零件的厚度x=
如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC:OA=1:2,且量得CD=12mm,则零件的厚度x=考点:相似三角形的应用
专题:
分析:利用两组对应边成比例,两三角形相似求出△OAB和△OCD相似,再根据相似三角形对应边成比例求出AB,然后求解即可.
解答:解:∵AC=BD,OC=OD,
∴OA=OB,
∴
=
,
又∵∠AOB=∠COD,
∴△OAB∽△OCD,
∴
=
=
,
∴AB=2CD=2×12=24,
∴x=
×(30-24)=3mm.
故答案为:3.
∴OA=OB,
∴
| OC |
| OA |
| OD |
| OB |
又∵∠AOB=∠COD,
∴△OAB∽△OCD,
∴
| CD |
| AB |
| OC |
| OA |
| 1 |
| 2 |
∴AB=2CD=2×12=24,
∴x=
| 1 |
| 2 |
故答案为:3.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,求出相似三角形是解题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(a2)3=a5 |
| B、a6÷a3=a2 |
| C、a2•a=a3 |
| D、(a-b)2=a2-b2 |
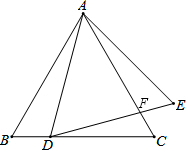 如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F. 如图,在△ABC中,AB=5,AC=4,△ABC绕着点A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之比为
如图,在△ABC中,AB=5,AC=4,△ABC绕着点A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之比为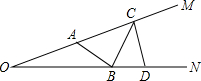 如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD的长AB+BC+CD的最小值是
如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD的长AB+BC+CD的最小值是