题目内容
 如图,小亮为了测出旗杆CD的高度,在平地上选择一点A,用测角仪测得旗杆顶端D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上),用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.求旗杆高CD(结果用根号表示).
如图,小亮为了测出旗杆CD的高度,在平地上选择一点A,用测角仪测得旗杆顶端D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上),用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.求旗杆高CD(结果用根号表示).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点B作BE⊥AD于点E,然后根据AB=40m,∠A=30°,可求得点B到AD的距离;再求出∠EBD的度数,然后求出AD的长度,然后根据∠A=30°即可求出CD的高度.
解答: 解:过点B作BE⊥AD于点E,
解:过点B作BE⊥AD于点E,
∵AB=40m,∠A=30°,
∴BE=
AB=20m,AE=
=20
m,
在Rt△ABE中,
∵∠A=30°,
∴∠ABE=60°,
∵∠DBC=75°,
∴∠EBD=180°-60°-75°=45°,
∴DE=EB=20m,
则AD=AE+EB=20
+20=20(
+1),
在Rt△ADC中,∠A=30°,
∴DC=
=10+10
.
答:塔高CD为(10+10
)m.
 解:过点B作BE⊥AD于点E,
解:过点B作BE⊥AD于点E,∵AB=40m,∠A=30°,
∴BE=
| 1 |
| 2 |
| AB2-BE2 |
| 3 |
在Rt△ABE中,
∵∠A=30°,
∴∠ABE=60°,
∵∠DBC=75°,
∴∠EBD=180°-60°-75°=45°,
∴DE=EB=20m,
则AD=AE+EB=20
| 3 |
| 3 |
在Rt△ADC中,∠A=30°,
∴DC=
| AD |
| 2 |
| 3 |
答:塔高CD为(10+10
| 3 |
点评:本题考查了解直角三角形的应用,难度适中,解答本题的关键是根据仰角构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
-1.5的倒数是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
 直线y=kx-6过点A(1,-4),与x轴交于点B,与y轴交于点D,以点A为顶点的抛物线经过点B,且交y轴于点C.
直线y=kx-6过点A(1,-4),与x轴交于点B,与y轴交于点D,以点A为顶点的抛物线经过点B,且交y轴于点C.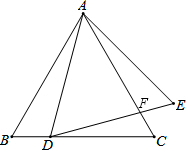 如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.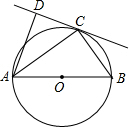 已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D.
已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D.