题目内容
13. 如图是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=16,则S2的值是$\frac{16}{3}$.
如图是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=16,则S2的值是$\frac{16}{3}$.
分析 根据八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,得出CG=NG,CF=DG=NF,再根据S1=(CG+DG)2,S2=GF2,S3=(NG-NF)2,S1+S2+S3=16得出3GF2=16,求出GF2的值即可.
解答 解:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
∴CG=NG,CF=DG=NF,
∴S1=(CG+DG)2
=CG2+DG2+2CG•DG
=GF2+2CG•DG,
S2=GF2,
S3=(NG-NF)2=NG2+NF2-2NG•NF,
∴S1+S2+S3=GF2+2CG•DG+GF2+NG2+NF2-2NG•NF=3GF2=16,
∴GF2=$\frac{16}{3}$,
∴S2=$\frac{16}{3}$.
故答案为$\frac{16}{3}$.
点评 此题主要考查了勾股定理的应用,用到的知识点是勾股定理和正方形、全等三角形的性质,根据已知得出3GF2=16是解决问题的关键.

练习册系列答案
相关题目
1.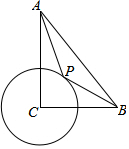 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2$\sqrt{17}$ | D. | 4 |
18.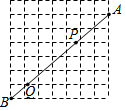 如图,在7×7的正方形网格中,连接两格点A,B,线段AB与其中两条网格线的交点为P,Q,则AP:PQ:QB的值为( )
如图,在7×7的正方形网格中,连接两格点A,B,线段AB与其中两条网格线的交点为P,Q,则AP:PQ:QB的值为( )
 如图,在7×7的正方形网格中,连接两格点A,B,线段AB与其中两条网格线的交点为P,Q,则AP:PQ:QB的值为( )
如图,在7×7的正方形网格中,连接两格点A,B,线段AB与其中两条网格线的交点为P,Q,则AP:PQ:QB的值为( )| A. | 2:3:1 | B. | 4:5:3 | C. | 2:4:1 | D. | 5:6:3 |

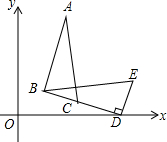 如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
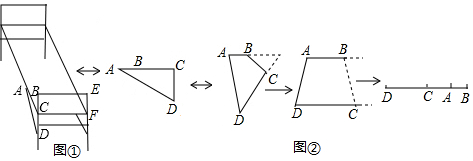
 如图,等边△ABC的边长为2,BD是高,延长BC到点E,使CE=CD,则DE的长为$\sqrt{3}$.
如图,等边△ABC的边长为2,BD是高,延长BC到点E,使CE=CD,则DE的长为$\sqrt{3}$.