题目内容
4.将一副等腰直角三角板拼成如图(1)所示的图形(说明:三角板有一锐角为45°),连结AD、BE.(1)BE与AD的数量关系是AD=BE(B、C、D在一条直线上);
(2)图(2)是三角板绕C点旋转了个角度,此时BE与AD的数量关系是否有所改变?请说明理由.

分析 (1)根据等腰三角形性质推出∠ACB=∠DCE=90°,AC=BC,CD=CE,根据SAS证明两三角形全等即可;
(2)根据全等三角形的判定和性质即可得到结论.
解答 解:(1)相等,
理由:在△ADC与△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE=90°}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴BE=AD;
故答案为:AD=BE;
(2)没有改变,
理由是:∵∠ACB=∠ECD,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
在△BCE和△ACD中,$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{EC=DC}\end{array}\right.$
∴△BCE≌△ACD,
∴BE=AD.
点评 本题考查了全等三角形的性质和判定,三角形的内角和定理的应用,主要培养学生运用定理进行推理的能力,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
12.下列运算中,结果正确的是( )
| A. | (x2)3=x5 | B. | 3x2+2x2=5x4 | C. | x3•x3=x6 | D. | (x+y)2=x2+y2 |
14.已知点A(1,3)、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为( )
| A. | (2,0) | B. | (2.5,0) | C. | (4,0) | D. | (4.5,0) |

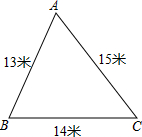 学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元? 如图是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=16,则S2的值是$\frac{16}{3}$.
如图是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=16,则S2的值是$\frac{16}{3}$.