题目内容
17.若二次函数y=-x2+4x+c的图象经过A(1,y1),B(-1,y2),C(2+$\sqrt{2}$,y3)三点,则y1、y2、y3的大小关系是( )| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y2<y1<y3 |
分析 先求出二次函数的对称轴为直线x=2,再判断出点A、B、C到对称轴的大小,然后根据二次函数的增减性,x<2,y随x的增大而增大,x>2时,y随x的增大而减小解答.
解答 解:∵y=-x2+4x+c=-x2+4x-4+4+c,
=-(x-2)2+4+c,
∴二次函数对称轴为直线x=2,
∵2-1=1,
2-(-1)=3,
2+$\sqrt{2}$-2=$\sqrt{2}$,
∴1<$\sqrt{2}$<3,
∴y2<y3<y1.
故选C.
点评 本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称轴与增减性.

练习册系列答案
相关题目
5.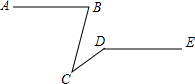 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
2. 如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:dm),可求得它的体积(单位:dm3)是( )
如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:dm),可求得它的体积(单位:dm3)是( )
 如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:dm),可求得它的体积(单位:dm3)是( )
如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:dm),可求得它的体积(单位:dm3)是( )| A. | 80 | B. | 240 | C. | 250 | D. | 480 |
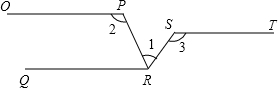 如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=40°.
如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=40°.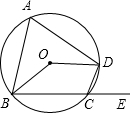 如图,四边形ABCD内接于⊙O,若∠BOD=130°,则它的一个外角∠DCE=65°.
如图,四边形ABCD内接于⊙O,若∠BOD=130°,则它的一个外角∠DCE=65°.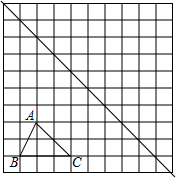 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)及直线l.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)及直线l.