题目内容
16.如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠ACB=90°,AC、BC的长分别是一元二次方程x2-14x+48=0的两个根(AC<BC).动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.(1)直接写出点C的坐标,C(0,4.8);当t=2.5秒时,动点M、N相遇;
(2)若点E在坐标轴上,平面内是否存在点F,使以点B、C、E、F为顶点的四边形是矩形?若存在,请直接写出点F的坐标若不存在,请说明理由.
(3)设△PMN的面积为S,求S与t之间的函数关系式以及自变量范围.

分析 (1)先求出AC、BC、AB、再根据$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•CO•AB求出OC即可解决问题.
(2)存在,如图1中,分两种情形讨论①当BC为对角线时,∵②当BC为边时,点E′在x轴上时或点E″在y轴上时,分别求出点F坐标即可.
(3)分三种情况求函数解析式,①0<t≤$\frac{7}{5}$,②$\frac{7}{5}$<t<$\frac{5}{2}$③$\frac{5}{2}$<t≤$\frac{10}{3}$先表示出MN,用相似借助OC,用时间表示出PG,面积即可确定.
解答 解:(1)∵AC、BC的长分别是一元二次方程x2-14x+48=0的两个根(AC<BC).
∴AC=6,BC=8,
∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
∵$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•CO•AB,
∴CO=4.8,
∴点C坐标(0,4.8),
设t秒后相遇,由题意(1+3)t=10,
∴t=2.5.
故答案分别为(0,4.8),=2.5.
(2)存在,如图1中,
①当BC为对角线时,∵OB=$\sqrt{B{C}^{2}-O{C}^{2}}$=$\sqrt{{8}^{2}-4.{8}^{2}}$=6.4,OA=3.6,
∴点F坐标(6.4,4.8).
②当BC为边时,点E′在x轴上时,点F坐标(2.8,-4.8);点E″在y轴上时,E″(0,-$\frac{128}{15}$),F″(-6.4,-$\frac{56}{15}$).
综上所述点F坐标为(6.4,4,8)或(2.8,-4.8)或(-6.4,-$\frac{56}{15}$).
(3)①如图2中,0<t≤$\frac{7}{5}$时,
∵PG∥CO,
∴$\frac{PG}{CO}$=$\frac{BG}{OB}$,
∴PG=$\frac{3}{4}$(t+5),
∴S=$\frac{1}{2}$•PG•MN=$\frac{3}{8}$(t+5)(10-4t)=-$\frac{3}{2}$t2-$\frac{15}{4}$t+$\frac{75}{4}$.
②如图3中,$\frac{7}{5}$<t<$\frac{5}{2}$时,
∵PG∥CO,
∴$\frac{PG}{CO}$=$\frac{AG}{AO}$,
∴PG=$\frac{4}{3}$(5-t),
∴S=$\frac{2}{3}$(5-t)(10-4t)=$\frac{8}{3}$t2-20t+$\frac{100}{3}$.
③如图4中,$\frac{5}{2}$<t≤$\frac{10}{3}$时,
S=$\frac{1}{2}$•MN•PG=$\frac{1}{2}$•(4t-10)•$\frac{4}{3}$(5-t)=-$\frac{8}{3}$t2+20t-$\frac{100}{3}$,
综上所述S=$\left\{\begin{array}{l}{-\frac{3}{2}{t}^{2}-\frac{15}{4}t+\frac{75}{4}}&{(0<t≤\frac{7}{5})}\\{\frac{8}{3}{t}^{2}-20t+\frac{100}{3}}&{(\frac{7}{5}<t<\frac{5}{2})}\\{-\frac{8}{3}{t}^{2}+20t-\frac{100}{3}}&{(\frac{5}{2}<t≤\frac{10}{3})}\end{array}\right.$.
点评 本题考查四边形综合题、矩形的判定和性质、平行线的性质等知识,解题的关键是灵活应用这些知识解决问题,学会分类讨论,确定分段函数的自变量取值范围是难点,需要画好图形结合图形解决问题,属于中考压轴题.

 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | $\frac{2}{9}$ | B. | $\frac{9}{4}$ | C. | $\frac{2}{3}$ | D. | $-\frac{2}{9}$ |
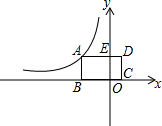 矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.
矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A. 如图所示,二次函数y=ax2+bx+c的图象中,陈刚同学观察得出了下面四条结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.其中正确的序号有①③④.
如图所示,二次函数y=ax2+bx+c的图象中,陈刚同学观察得出了下面四条结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.其中正确的序号有①③④.