题目内容
14.一次函数y=kx+b的图象与x轴、y轴的交点坐标分别是(-2,0),(0,-1),这个一次函数的解析式为( )| A. | y=$\frac{1}{2}$x-1 | B. | y=2x+2 | C. | y=-x-1 | D. | y=2x-1 |
分析 设一次函数的解析式为y=kx+b(k≠0),再把(-2,0),(0,-1)代入求出k、b的值即可.
解答 解:设一次函数的解析式为y=kx+b(k≠0),
∵函数图象与x轴、y轴的交点坐标分别是(-2,0),(0,-1),
∴$\left\{\begin{array}{l}-2k+b=0\\ b=-1\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{1}{2}\\ b=-1\end{array}\right.$,
∴一次函数的解析式为y=$\frac{1}{2}$x-1.
故选A.
点评 本题考查的是一次函数的图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若二次函数y=ax2的图象经过点P(-3,2),则a的值为( )
| A. | $\frac{2}{9}$ | B. | $\frac{9}{4}$ | C. | $\frac{2}{3}$ | D. | $-\frac{2}{9}$ |
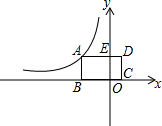 矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.
矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.
