题目内容
13.观察并探求下列各问题,写出你所观察得到的结论,并说明理由.
(1)如图①,△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由.
(2)将(1)中点P移至△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)将(2)中点P变为两个点P1、P2得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
(4)将(3)中的点P1、P2移至△ABC外,并使点P1、P2与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB,得图④,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
分析 (1)、(2)、(3)通过作辅助线,利用三角形的第三边小于两边之和,大于两边之差进行解答即可;
(4)通过将四边形BP1P2C沿直线BC翻折,使点P1、P2落在△ABC内,转化为(3)情形,从而问题得解.
解答 解:(1)BP+PC<AB+AC,理由如下:
在△ABC中,根据三角形两边之和大于第三边,得:BC<AB+AC,
即BP+PC<AB+AC;
(2)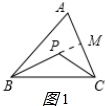 △BPC的周长<△ABC的周长.理由如下:
△BPC的周长<△ABC的周长.理由如下:
如图1,延长BP交AC于M,
在△ABM中,BP+PM<AB+AM,
在△PMC中,PC<PM+MC,
两式相加得BP+PC<AB+AC,
∴BP+PC+BC<AB+AC+BC,
即△BPC的周长<△ABC的周长.
(3)四边形BP1P2C的周长<△ABC的周长.理由如下:
如图2,分别延长BP1、CP2交于M,
由(2)知,BM+CM<AB+AC,又P1P2<P1M+P2M,
可得,BP1+P1P2+P2C<BM+CM<AB+AC,
∴BP1+P1P2+P2C+BC<BM+CM<AB+AC+BC,
即四边形BP1P2C的周长<△ABC的周长.
(4)四边形BP1P2C的周长<△ABC的周长.理由如下:
将四边形BP1P2C沿直线BC翻折,使点P1、P2落在△ABC内,
转化为(3)情形,
同(3)得:四边形BP1P2C的周长<△ABC的周长.
点评 本题是三角形综合题目,考查了三角形的三边关系、三角形和四边形周长的计算;比较线段的长短常常利用三角形的三边关系以及不等式的性质,通过作辅助线进是解决问题的关键.

练习册系列答案
相关题目
5.若二次函数y=ax2的图象经过点P(-3,2),则a的值为( )
| A. | $\frac{2}{9}$ | B. | $\frac{9}{4}$ | C. | $\frac{2}{3}$ | D. | $-\frac{2}{9}$ |
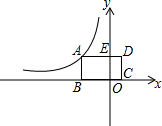 矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.
矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A. 如图所示,二次函数y=ax2+bx+c的图象中,陈刚同学观察得出了下面四条结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.其中正确的序号有①③④.
如图所示,二次函数y=ax2+bx+c的图象中,陈刚同学观察得出了下面四条结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.其中正确的序号有①③④.
 在如图所示的方格纸中,画出将图中△ABC向右平移4格后的△A′B′C′.
在如图所示的方格纸中,画出将图中△ABC向右平移4格后的△A′B′C′.