题目内容
16.解不等式组:$\left\{\begin{array}{l}3(x-1)<6x\\ \frac{x+1}{2}≥2x\end{array}\right.$.分析 先分别解两个不等式得到x>-1和x≤$\frac{1}{3}$,然后根据大小小大中间找确定不等式组的解集.
解答 解:$\left\{\begin{array}{l}{3(x-1)<6x①}\\{\frac{x+1}{2}≥2x②}\end{array}\right.$,
解①得x>-1,
解②得x≤$\frac{1}{3}$,
所以不等式组的解集为-1<x≤$\frac{1}{3}$.
点评 本题考查了解不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
1.下列命题:
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直平分且相等的四边形是正方形
④一组对边相等,另一组对边平行的四边形是平行四边形
其中正确的有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直平分且相等的四边形是正方形
④一组对边相等,另一组对边平行的四边形是平行四边形
其中正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.某课外兴趣小组为了解所在地区的老年人的健康状况,分别作了四种不同的抽样调查,你认为抽样较合理的是( )
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 在医院调查了1000名老年人的健康状况 | |
| C. | 调查了100名小区内老年邻居的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 |
 如图所示,在正方形ABCD的对角线AC上取点E,使CD=CE,过点E作EF⊥AC交AD于点F,求证:AE=EF=DF.
如图所示,在正方形ABCD的对角线AC上取点E,使CD=CE,过点E作EF⊥AC交AD于点F,求证:AE=EF=DF.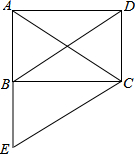 已知:如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.求证:AC=EC.
已知:如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.求证:AC=EC.