题目内容
3.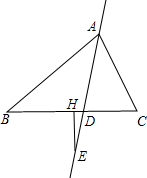 如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系.
如图,在△ABC中,AD平分∠CAB,点E是直线AD上的动点(H点不与D点重合),过点E作BC的垂线段EH,探索∠DEH,∠B,∠C之间的关系.
分析 根据三角形内角和定理用∠B、∠C表示∠BAC,根据角平分线的定义表示∠DAC,再根据三角形内角和定理表示∠ADC,根据对顶角相等和垂直的定义,得到答案.
解答 解:∵∠BAC=180°-∠B-∠C,AD平分∠CAB,
∴∠DAC=$\frac{1}{2}$(180°-∠B-∠C),
∴∠ADC=180°-∠C-$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠C+$\frac{1}{2}$∠B,
∵EH⊥BC,∠HDE=∠ADC,
∴∠DEH=90°-(90°-$\frac{1}{2}$∠C+$\frac{1}{2}$∠B)=$\frac{1}{2}$(∠C-∠B).
点评 本题考查的是三角形内角和定理、对顶角相等和垂直的定义,掌握三角形内角和是180°是解题的关键,解答时,注意解题步骤的规范性.

练习册系列答案
相关题目
14.某运动器械厂根据市场需求,计算生产A、B两种型号的按摩椅,某部分信息如下:A、B两种型号的按摩椅共生产40台,该厂所筹生产按摩椅的资金不少于90万元,但不超过91万元,且所筹资金全部用于这两种按摩椅,现已知A、B两种按摩椅的生产成本和售价如表:
根据以上信息,解答下列问题:
(1)该公司对此两种按摩椅有几种生产方案?那种生产方案获得最大利润?
(2)据市场调查,每台A型按摩椅的售价将会提高a万元(a>0),每台B型按摩椅售价不会改变,该公司应如何生产才可以获得最大利润?
| 型号 | 成本(万元/台) | 售价(万元/台) |
| A | 2 | 2.4 |
| B | 2.5 | 3 |
(1)该公司对此两种按摩椅有几种生产方案?那种生产方案获得最大利润?
(2)据市场调查,每台A型按摩椅的售价将会提高a万元(a>0),每台B型按摩椅售价不会改变,该公司应如何生产才可以获得最大利润?
18.若函数y=x2-2x-1的图象与x轴的交点为(x1,0)和(x2,0),则x12x2+x1x22的值为( )
| A. | -2 | B. | 1 | C. | $\sqrt{2}$-1 | D. | -1-$\sqrt{2}$ |
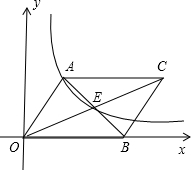 如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.
如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.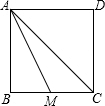 如图,正方形ABCD中,点M是边BC上的中点,联结AM,AC,则sin∠MAC=$\frac{\sqrt{10}}{5}$.
如图,正方形ABCD中,点M是边BC上的中点,联结AM,AC,则sin∠MAC=$\frac{\sqrt{10}}{5}$. 如图所示,在正方形ABCD的对角线AC上取点E,使CD=CE,过点E作EF⊥AC交AD于点F,求证:AE=EF=DF.
如图所示,在正方形ABCD的对角线AC上取点E,使CD=CE,过点E作EF⊥AC交AD于点F,求证:AE=EF=DF. 如图,等边三角形ABC的边长为6cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、PN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<3),四边形MNQP的面积为S cm2.
如图,等边三角形ABC的边长为6cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、PN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<3),四边形MNQP的面积为S cm2.