题目内容
2．
如图，在△ABC中，AD为BC边上的中线，延长AD至E，使DE=AD，连接BE，CE．（1）请判断四边形ABEC的形状；
（2）当△ABC满足什么条件时，四边形ABEC是矩形？
分析 （1）由已知条件得出BD=CD，再由DE=AD，即可证出四边形ABEC是平行四边形；
（2）由矩形的定义即可得出结论．
解答 解：（1）四边形ABEC是平行四边形；理由如下：
∵AD为BC边上的中线，
∴BD=CD，
∵DE=AD，
∴四边形ABEC是平行四边形（对角线互相平分的四边形是平行四边形）；
（2）当∠BAC=90°，四边形ABEC是矩形；理由如下：
∵四边形ABEC是平行四边形，∠BAC=90°，
∴四边形ABEC是矩形（有一个角是直角的平行四边形是矩形）．
点评 本题考查了平行四边形的判定、矩形的判定；熟练掌握平行四边形和矩形的判定方法，并能进行推理论证是解决问题的关键．
练习册系列答案
相关题目
如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：
求阴影部分的面积．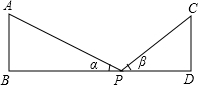
如图，在水平地面上有两座高度相同的高压电缆，铁搭AB和CD两塔底B和D之间的距离为87米，在两塔底连结BD上取一点P，测得两塔顶A和C的仰角分别为α和β，如果tanα=$\frac{3}{4}$，tanβ=$\frac{12}{13}$，求铁搭的高度．
11．在△ABC中，AB=AC．
（1）若D为AC的中点，BD把三角形的周长分别24cm和30cm两部分，求△ABC三边的长．
（2）若D为AC上一点，试说明AC＞$\frac{1}{2}$（BD+DC）
（1）若D为AC的中点，BD把三角形的周长分别24cm和30cm两部分，求△ABC三边的长．
（2）若D为AC上一点，试说明AC＞$\frac{1}{2}$（BD+DC）
12．一个二次函数，当x=0时，y=-5，当x=-1时，y=-4，当x=2时，y=5，则这个二次函数的解析式是（ ）
| A． | y=2x2-x-5 | B． | y=2x2+x+5 | C． | y=2x2-x+5 | D． | y=2x2+x-5 |