题目内容
6.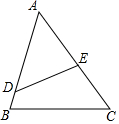 如图,∠ADE=∠C,AD=CE=2,AE=1,求$\frac{DE}{BC}$的值.
如图,∠ADE=∠C,AD=CE=2,AE=1,求$\frac{DE}{BC}$的值.
分析 求出AC长,根据相似三角形的判定推出△ADE∽△ACB,根据相似三角形的性质得出比例式,代入求出即可.
解答 解:∵AE=1,CE=2,
∴AC=AE+CE=2+1=3,
∵∠ADE=∠C,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{BC}$,
∵AD=2,AC=3,
∴$\frac{DE}{BC}$=$\frac{2}{3}$.
点评 本题考查了相似三角形的性质和判定,能根据已知推出△ADE∽△ACB是解此题的关键.

练习册系列答案
相关题目
17.对于任意大于或等于4的偶数,存在下列勾股数:
(1)根据以上规律,请你直接写出第7组勾股数:
(2)请你猜想出第n组(n为正整数),并证明这是一组勾股数.
| 组别 | a | b | c |
| 第1组 | 4=2×2 | 3=22-1 | 5=22+1 |
| 第2组 | 6=2×3 | 8=32-1 | 10=32+1 |
| 第3组 | 8=2×4 | 15=42-1 | 17=42+1 |
(2)请你猜想出第n组(n为正整数),并证明这是一组勾股数.
11.下列说法错误的有( )
①1的平方根与立方根都是1
②大于1小于2的无理数只有$\sqrt{2}$和$\sqrt{3}$
③单项式-πa2b的次数是4
④x=1是方程2+$\frac{\sqrt{3}x-3}{3}$=$\frac{\sqrt{3}}{3}$+1的解.
①1的平方根与立方根都是1
②大于1小于2的无理数只有$\sqrt{2}$和$\sqrt{3}$
③单项式-πa2b的次数是4
④x=1是方程2+$\frac{\sqrt{3}x-3}{3}$=$\frac{\sqrt{3}}{3}$+1的解.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列各式中,正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | ±$\sqrt{9}$=±3 | C. | $\root{3}{-9}$=-3 | D. | (-$\sqrt{3}$)2=9 |
15.如果三角形的两边分别为3和5,那么第三边可能是( )
| A. | 3 | B. | 1 | C. | 2 | D. | 8 |
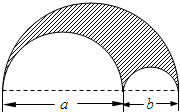 如图,一块直径为a+b的半圆形钢板,从中挖去直径分别为a与b的两个半圆
如图,一块直径为a+b的半圆形钢板,从中挖去直径分别为a与b的两个半圆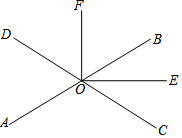 如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=114°,求∠BOF的度数.
如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=114°,求∠BOF的度数.