题目内容
17.某市居民用电收费有两种方式,普通电价:全天0.53元/千瓦时,峰谷电价:峰时(早8:00~晚22:00)电价0.57元/千瓦时,谷时(晚22:00~早8:00)电价分为三级:第一级50千瓦时及以下的部分,电价为0.29元/千瓦时,超过50千瓦时,不超过200千瓦时为第二级,超过部分的电价为0.32元/千瓦时;超过200千瓦时为第三级,超过部分的电价为0.39元/千瓦时.小明家使用的是峰谷电.(1)小明家上个月总用电量为250千瓦时,其中峰时用电量为100千瓦时,问小明家上月应付电费是多少元?与普通电价相比,是便宜了还是贵了?
(2)若小明家一个月峰时电量为100千瓦时,谷时电量为m千瓦时(100<m≤200),请用含m的代数式表示小明家该月应交的电费.
(3)某月小明家的电费为215.5元,其中峰时电量为200千瓦时,问那个月小明家的总用电量是多少千瓦时.
分析 (1)根据题意可以得到小明家上月应付的电费和按普通价格需付的电费,从而可以解答本题;
(2)根据题意可以用含m的代数式表示小明家该月应交的电费;
(3)根据题意可以判断小明家的用电量,从而可以根据题意列出相应的方程,进而解答本题.
解答 解:(1)由题意可得,
小明家上月应付电费为:0.57×100+[50×0.29+(250-100-50)×0.32]=103.5(元),
如果按普通电价应付电费为:250×0.53=132.5(元),
∵132.5>103.5,
∴与普通电价相比,便宜了,
即小明家上月应付电费是101.5元,与普通电价相比,便宜了;
(2)由题意可得,
小明家该月应交的电费为:0.57×100+[50×0.29+(m-50)×0.32]=0.32m+55.5,
即小明家该月应交的电费为(0.32m+55.5)元;
(3)由题意可得,
小明家峰时的电费为:200×0.57=114(元),
若谷时的用电量为50时,需交电费为:50×0.29=14.5,则114+14.5<215.5,故此种情况不符合要求,
若谷时的用电量为200时,需交电费为:50×0.29+(200-50)×0.32=62.5,114+62.5=176.5<215.5,故此种情况不符合要求,
∴小明家这个月用电量在谷时超过200千瓦时,
设小明家这个月的用电量为x千瓦时,
200×0.57+50×0.29+(200-50)×0.32+(x-200-200)×0.39=215.5,
解得,x=500,
即那个月小明家的总用电量是500千瓦时.
点评 本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程,找出所求问题需要的条件.

练习册系列答案
相关题目
14.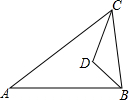 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )| A. | 30° | B. | 32° | C. | 36° | D. | 40° |
9.若正比例函数y=kx与反比例函数y=$\frac{{k}^{′}}{x}$的一个交点坐标为(-2,3),则另一个交点为( )
| A. | (-2,-3) | B. | (2,3) | C. | (2,-3) | D. | (3,2) |
6.下列等式中成立的是( )
| A. | a4•a=a4 | B. | a6-a3=a3 | C. | (ab2)3=a3•b5 | D. | (a3)2=a6 |
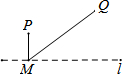
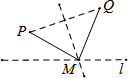
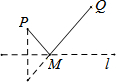
 如图:已知△ABC中,AD是中线,且∠1=∠2,求证:AB=AC.
如图:已知△ABC中,AD是中线,且∠1=∠2,求证:AB=AC.