题目内容
8.已知当-1<x<0时,二次函数y=x2-3mx+2的值恒大于1,求m的取值范围.分析 将x=-1代入函数的解析式,令y>1即可求得m的取值范围.
解答 解:二次函数y=x2-3mx+2的图象是一条开口向上的抛物线,
(1)当抛物线的对称轴x=$\frac{3}{2}$m≤-1时,即m≤-$\frac{2}{3}$,
要使二次函数解析式的值-1<x<0时恒大于1,只要
x=-1,y=1+3m+2=3m+3≥1,
解得:m≥-$\frac{2}{3}$,
∴m=-$\frac{2}{3}$,
(2)当抛物线的对称轴x=$\frac{3}{2}$m≥0时,即m≥0时,
要使二次函数解析式的值-1<x<0时恒大于1,只要m≥0即可;
(3)当抛物线的对称轴x=$\frac{3}{2}$m在区间-1<x<0时,
∵-1<$\frac{3}{2}$m<0,
∴-$\frac{2}{3}$<m<0,
综上所述:m的取值范围是:m≥-$\frac{2}{3}$.
点评 本题主要考查的是二次函数的性质和二次函数的最值,掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
5.下列命题中,假命题是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对角分别相等的四边形是平行四边形 | |
| C. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| D. | 对角线相等的平行四边形是矩形 |
18.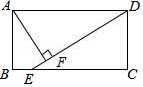 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )| A. | AF=$\frac{1}{2}$AD | B. | AB=AF | C. | △AFD≌△DCE | D. | BE=AD-DF |
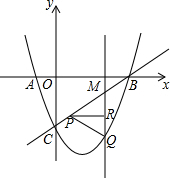 如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )



