题目内容
 已知直角坐标系中有两点A(-1,2)、B(5,4),要在x轴上找一点P,使得PA+PB之和最小,求点P的坐标.
已知直角坐标系中有两点A(-1,2)、B(5,4),要在x轴上找一点P,使得PA+PB之和最小,求点P的坐标.考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:先求出点A关于x轴的对称点A′的坐标,连接A′B交x轴于P,此时PA+PB最小,用待定系数法求出直线A′B的解析式,然后求出直线与x轴的交点即可.
解答:解:∵A(-1,2),
∴点A关于x轴的对称点A′的坐标为(-1,-2),
∵A′(-1,-2),B(5,4),
设直线A′B的解析式为y=kx+b(k≠0),
∴
,
解得
,
∴直线A′B的解析式为y=x-1,
当y=0时,x=1.
∴P(1,0).
∴点A关于x轴的对称点A′的坐标为(-1,-2),
∵A′(-1,-2),B(5,4),
设直线A′B的解析式为y=kx+b(k≠0),
∴
|
解得
|
∴直线A′B的解析式为y=x-1,
当y=0时,x=1.
∴P(1,0).
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,平行四边形ABCD中,E为DC的中点,AC与BE交于点F.则△EFC与△BFA的面积比为( )
如图,平行四边形ABCD中,E为DC的中点,AC与BE交于点F.则△EFC与△BFA的面积比为( )A、1:
| ||
| B、1:2 | ||
| C、1:4 | ||
| D、1:8 |
 如图,∠B=62°,∠3=30°,∠4=88°,AB与CD平行吗?AD与BC平行吗?
如图,∠B=62°,∠3=30°,∠4=88°,AB与CD平行吗?AD与BC平行吗?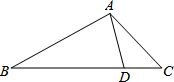 如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为
如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为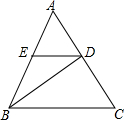 已知:如图,BD是等腰三角形ABC的底边AC上的高,∠ADE=∠C.求证:△BDE是等腰三角形.
已知:如图,BD是等腰三角形ABC的底边AC上的高,∠ADE=∠C.求证:△BDE是等腰三角形.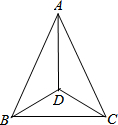 如图,已知在△ABC中,AB=AC,点D是△ABC内一点,且∠ABD=∠ACD,求证:AD是∠BAC的平分线.
如图,已知在△ABC中,AB=AC,点D是△ABC内一点,且∠ABD=∠ACD,求证:AD是∠BAC的平分线.
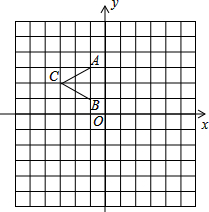 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)