题目内容
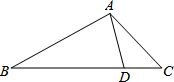 如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为
如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为考点:相似三角形的判定与性质
专题:
分析:首先在△ABC和△DAC中根据题干条件得到
=
=
,结合∠ACB=∠DCA,证明出△ABC∽△DAC,进而得到AD的长.
| AC |
| BC |
| DC |
| AC |
| 1 |
| 2 |
解答:解:在△ABC和△DAC,
∵AC=4,BC=8,CD=2,
∴
=
=
,
∵∠ACB=∠DCA,
∴△ABC∽△DAC,
∴
=
=
,
∵AB=6,
∴AD=3,
故答案为3.
∵AC=4,BC=8,CD=2,
∴
| AC |
| BC |
| DC |
| AC |
| 1 |
| 2 |
∵∠ACB=∠DCA,
∴△ABC∽△DAC,
∴
| AD |
| AB |
| AC |
| AB |
| 1 |
| 2 |
∵AB=6,
∴AD=3,
故答案为3.
点评:本题主要考查了相似三角形的判定与性质的知识,解答本题的关键是根据题干条件证明出△ABC∽△DAC,此题难度不大.

练习册系列答案
相关题目
在一次扶贫助残活动中,共捐款2 580 000元.将2 580 000用科学记数法表示为( )
| A、2.58×107 |
| B、0.258×107 |
| C、25.8×106 |
| D、2.58×106 |
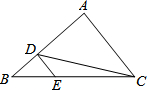 如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )
如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )| A、1:5 | B、1:9 |
| C、1:10 | D、1:12 |
 如图,△ABC中,D,E两点分别在AB,AC上,且AD=12,DB=16,AE=16,EC=5.若M,N分别为DE和BC的中点,则AM:AN=
如图,△ABC中,D,E两点分别在AB,AC上,且AD=12,DB=16,AE=16,EC=5.若M,N分别为DE和BC的中点,则AM:AN=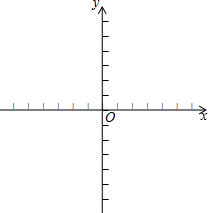 已知直角坐标系中有两点A(-1,2)、B(5,4),要在x轴上找一点P,使得PA+PB之和最小,求点P的坐标.
已知直角坐标系中有两点A(-1,2)、B(5,4),要在x轴上找一点P,使得PA+PB之和最小,求点P的坐标.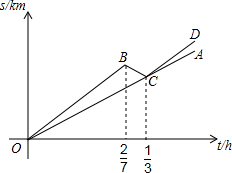 某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.
某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.