题目内容
如图1,△ABC中,BC=25,BC边上的高为20,将AB,AC分别n等分,连接两边对应的等分点,以这些连接线为一边作矩形,使这些矩形的边B1C1,B2C2,B3C3…的对应边分别为 B2C2,B3C3,B4C4…
(1)若n=5,如图2,求B3C3为一边的矩形的面积;
(2)若n=5,求所有矩形的面积和;
(3)当分为n等分时,你能用含有n的表达式表示所有矩形的面积和吗?猜想当n越大时时所有矩形的面积和接近哪个值.
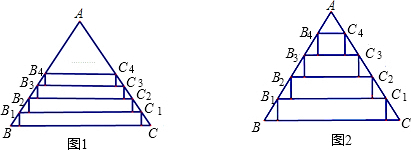
(1)若n=5,如图2,求B3C3为一边的矩形的面积;
(2)若n=5,求所有矩形的面积和;
(3)当分为n等分时,你能用含有n的表达式表示所有矩形的面积和吗?猜想当n越大时时所有矩形的面积和接近哪个值.

考点:相似三角形的判定与性质
专题:
分析:(1)利用相似三角形的判定与性质得出
=
=
,
=
=
,
=
=
,
=
=
,进而得出矩形的边长即可得出答案;
(2)利用(1)中所求进而得出其面积和;
(3)当分割为n分时,同(1)推理可知:B1C1=25×
,B2C2=25×
,B3C3=25×
,…Bn-1Cn-1=25×
,进而求出其面积和,再得出近似值.
| B1C1 |
| BC |
| AE |
| AD |
| 4 |
| 5 |
| B2C2 |
| BC |
| AF |
| AD |
| 3 |
| 5 |
| B3C3 |
| BC |
| AG |
| AD |
| 2 |
| 5 |
| B4C4 |
| BC |
| AH |
| AD |
| 1 |
| 5 |
(2)利用(1)中所求进而得出其面积和;
(3)当分割为n分时,同(1)推理可知:B1C1=25×
| n-1 |
| n |
| n-2 |
| n |
| n-3 |
| n |
| 1 |
| n |
解答: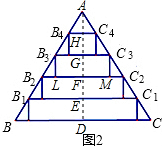 解:(1)过A作AD⊥BC于D,交B1C1于E,交B2C2于F,交B3C3于G,交B4C4于H,则
解:(1)过A作AD⊥BC于D,交B1C1于E,交B2C2于F,交B3C3于G,交B4C4于H,则
AD⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴
=
=
,
=
=
,
=
=
,
=
=
,
∵AD=20,BC=25,
∴B1C1=20,B2C2=15,B3C3=10,B4C4=5,AH=4,AG=8,AF=12,AE=16,
∴HG=GF=EF=ED=4,
∴矩形B3C3ML的面积为40;
(2)由(1)得所有矩形的面积和为:(5+10+15+20)×4=200;
(3)当分割为n分时,同(1)推理可知:
=
,
=
,
=
,
=
,…
=
,
则B1C1=25×
,B2C2=25×
,B3C3=25×
,…Bn-1Cn-1=25×
,
则每个小矩形的高为:
,
故所有矩形的面积和为:
(25×
+25×
+25×
+…+25×
)×
=
(n-1+n-2+…+1)×
=
×
×
=
,
故当n越大时所有矩形面积之和接近250.
 解:(1)过A作AD⊥BC于D,交B1C1于E,交B2C2于F,交B3C3于G,交B4C4于H,则
解:(1)过A作AD⊥BC于D,交B1C1于E,交B2C2于F,交B3C3于G,交B4C4于H,则AD⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴
| B1C1 |
| BC |
| AE |
| AD |
| 4 |
| 5 |
| B2C2 |
| BC |
| AF |
| AD |
| 3 |
| 5 |
| B3C3 |
| BC |
| AG |
| AD |
| 2 |
| 5 |
| B4C4 |
| BC |
| AH |
| AD |
| 1 |
| 5 |
∵AD=20,BC=25,
∴B1C1=20,B2C2=15,B3C3=10,B4C4=5,AH=4,AG=8,AF=12,AE=16,
∴HG=GF=EF=ED=4,
∴矩形B3C3ML的面积为40;
(2)由(1)得所有矩形的面积和为:(5+10+15+20)×4=200;
(3)当分割为n分时,同(1)推理可知:
| B1C1 |
| BC |
| n-1 |
| n |
| B2C2 |
| BC |
| n-2 |
| n |
| B3C3 |
| BC |
| n-3 |
| n |
| B4C4 |
| BC |
| n-4 |
| n |
| Bn-1Cn-1 |
| BC |
| 1 |
| n |
则B1C1=25×
| n-1 |
| n |
| n-2 |
| n |
| n-3 |
| n |
| 1 |
| n |
则每个小矩形的高为:
| 20 |
| n |
故所有矩形的面积和为:
(25×
| n-1 |
| n |
| n-2 |
| n |
| n-3 |
| n |
| 1 |
| n |
| 20 |
| n |
=
| 25 |
| n |
| 20 |
| n |
=
| 25 |
| n |
| (n-1)n |
| 2 |
| 20 |
| n |
=
| 250(n-1) |
| n |
故当n越大时所有矩形面积之和接近250.
点评:此题主要考查了相似三角形的判定与性质以及矩形的面积求法等知识,表示出矩形的长与宽是解题关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
使分式
有意义的条件是( )
| 2 |
| 2-x |
| A、x≠2 | B、x≠-2 |
| C、x>2 | D、x≠0 |
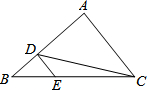 如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )
如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )| A、1:5 | B、1:9 |
| C、1:10 | D、1:12 |
 已知直角坐标系中有两点A(-1,2)、B(5,4),要在x轴上找一点P,使得PA+PB之和最小,求点P的坐标.
已知直角坐标系中有两点A(-1,2)、B(5,4),要在x轴上找一点P,使得PA+PB之和最小,求点P的坐标.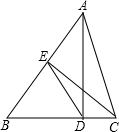 如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE.
如图,在△ABC中,AD⊥BC,CE⊥AB,D,E为垂足,联结DE. 每个小正方形边长均为1,求四边形ABCD的边长和面积.
每个小正方形边长均为1,求四边形ABCD的边长和面积.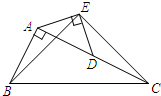 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试判断△BCE的形状,并证明你的结论.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试判断△BCE的形状,并证明你的结论.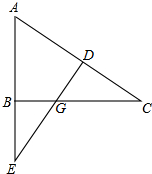 已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证:
已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证: