题目内容
1．已知$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=6}\\{nx+my=1}\end{array}\right.$的解，则代数式$\frac{m+n}{m-n}$的值是$\frac{1}{5}$．分析 把x与y的值代入方程组求出m与n的值，代入原式计算即可得到结果．
解答 解：把$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$代入方程组得：$\left\{\begin{array}{l}{4m+3n=6①}\\{3m+4n=1②}\end{array}\right.$，
①+②得：7（m+n）=7，即m+n=1，
①-②得：m-n=5，
则原式=$\frac{1}{5}$，
故答案为：$\frac{1}{5}$
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．
练习册系列答案
阅读快车系列答案
相关题目
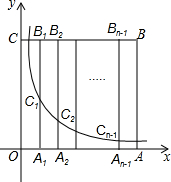如图，边长为n（n为正整数）的正方形OABC的边OA、OC在坐标轴上，点A1，A2，…，An-1为OA的n等分点，点B1，B2，B3…，Bn-1为CB的n等分点，连接A1B1，A2B2，A3B3，…，An-1Bn-1，分别与曲线y=$\frac{n-8}{x}$（x＞0）相交于点C1，C2，C3…，Cn-1．若B6C6=9A6C6，则n的值是20．
14．
如图，边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上，顶点D在反比例函数$y=\frac{k}{x}（x＞0）$的图象上，已知点B的坐标是$（{\frac{3}{4}，\frac{9}{4}}）$，则k的值为（ ）
如图，边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上，顶点D在反比例函数$y=\frac{k}{x}（x＞0）$的图象上，已知点B的坐标是$（{\frac{3}{4}，\frac{9}{4}}）$，则k的值为（ ）| A． | $\frac{27}{16}$ | B． | $\frac{27}{8}$ | C． | 4 | D． | 6 |