题目内容
12.一个不透明的盒子中装有两个白色乒乓球和一个黄色乒乓球,它们只有颜色的不同,甲、乙两人玩摸球游戏,每次只能摸出一个球.规则如下:甲摸一次,摸到黄乒乓球,得1分,否则得0分;乙摸两次,先摸出1个球,放回后,再摸出1个球,如果两次摸到的都是白色乒乓球,则得1分,否则不得分,得分多者获胜,如果平分,则再来一次,问此游戏是否公平,并请通过计算说明理由.分析 直接利用概率公式分别求出甲、乙得1分的概率,进而比较得出答案.
解答 解:此游戏不公平,
理由:∵一个不透明的盒子中装有两个白色乒乓球和一个黄色乒乓球,
∴甲摸一次,摸到黄乒乓球的概率为:$\frac{1}{3}$,故P(甲得1分)=$\frac{1}{3}$;
∵乙摸两次,先摸出1个球,放回后,再摸出1个球,如果两次摸到的都是白色乒乓球,则得1分,否则不得分,
∴列举出所有的可能: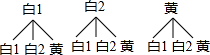 ,
,
故一共有9种可能,则两次摸到的都是白色乒乓球的概率为:$\frac{4}{9}$,
故P(乙得1分)=$\frac{4}{9}$;
∴P(乙得1分)>P(甲得1分),
∴此游戏不公平.
点评 此题主要考查了游戏公平性,正确列举出所有的可能是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.方程组$\left\{\begin{array}{l}{x-y=1}\\{x+y=3}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
7.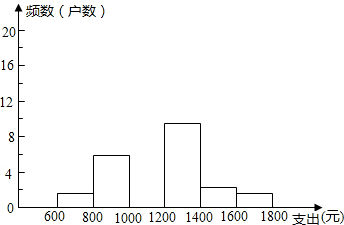 在今年“五一”期间,某学校团委要求学生参加一项社会调查活动,七年级学生小青想了解她所居住的小区500户居民每个月用于食品支出的情况,她从中随机调查了40户居民每个月用于食品支出的情况(支出取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
在今年“五一”期间,某学校团委要求学生参加一项社会调查活动,七年级学生小青想了解她所居住的小区500户居民每个月用于食品支出的情况,她从中随机调查了40户居民每个月用于食品支出的情况(支出取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题.
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭每个月用于食品支出较少(不足1200元)的户数大约有多少户?
 在今年“五一”期间,某学校团委要求学生参加一项社会调查活动,七年级学生小青想了解她所居住的小区500户居民每个月用于食品支出的情况,她从中随机调查了40户居民每个月用于食品支出的情况(支出取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
在今年“五一”期间,某学校团委要求学生参加一项社会调查活动,七年级学生小青想了解她所居住的小区500户居民每个月用于食品支出的情况,她从中随机调查了40户居民每个月用于食品支出的情况(支出取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.| 分组 | 划记 | 频数 |
| 800-999 |  | 2 |
| 1000-1199 |  | 6 |
| 1200-1399 |  | |
| 1400-1599 |  | 9 |
| 1600-1799 |  | |
| 1800-2000 |  | 2 |
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭每个月用于食品支出较少(不足1200元)的户数大约有多少户?
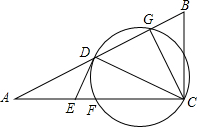 如图所示,在△ABC中,∠ACB=90°,D,F分别为AB,AC的中点,过D,F,C三点的⊙O交AB于点G,连接CG,CD,作DE⊥CD,交AC于点E.
如图所示,在△ABC中,∠ACB=90°,D,F分别为AB,AC的中点,过D,F,C三点的⊙O交AB于点G,连接CG,CD,作DE⊥CD,交AC于点E.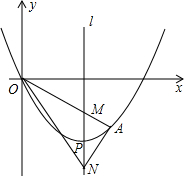 如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM. 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.