题目内容
2. 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.
分析 设△ADG面积为S,根据异底同高的时间面积之比等于底的比,分别求出△ADC、△DGE的面积即可解决问题.
解答  解:设△ADG面积为S,
解:设△ADG面积为S,
∵AG:GE=2:1,
∴S△ADG:S△DGE=2:1,
∴S△DGE=$\frac{1}{2}$S,
∵四边形DEBF是矩形,
∴DF∥GB,
∴DC:DG=CF:FB=2:3,
∴S△ACD:S△ADG=2:3,
∴S△ADC=$\frac{2}{3}$S,
∴$\frac{{S}_{△DGE}}{{S}_{△ADC}}$=$\frac{\frac{1}{2}S}{\frac{2}{3}S}$=$\frac{1}{3}$.
点评 本题考查矩形的性质、平行线分线段成比例定理等知识,解题的关键是设未知数,求出相应三角形面积,记住异底同高的时间面积之比等于底的比,属于中考常考题型.

练习册系列答案
相关题目
13.为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这一天5路公共汽车平均每班的载客量是多少?
请阅读下列探究问题,回答下列问题:
(1)这里的组中值指什么,它是怎样确定的?组中值是上下限之间的中点数值,组中值是指这个小组的两个端点的数的平均数
(2)第二组数据的频数5指什么呢?载客量x落在21≤x<41中的数据个数
(3)如果每组数据在本组中分布较为均匀,则各组数据的平均值和组中值有什么关系.相等.
| 载客量/人 | 组中值 | 频数(班次) |
| 1≤x<21 | 11 | 3 |
| 21≤x<41 | 31 | 5 |
| 41≤x<61 | 51 | 20 |
| 61≤x<81 | 71 | 22 |
| 81≤x<101 | 91 | 18 |
| 101≤x<121 | 111 | 15 |
请阅读下列探究问题,回答下列问题:
(1)这里的组中值指什么,它是怎样确定的?组中值是上下限之间的中点数值,组中值是指这个小组的两个端点的数的平均数
(2)第二组数据的频数5指什么呢?载客量x落在21≤x<41中的数据个数
(3)如果每组数据在本组中分布较为均匀,则各组数据的平均值和组中值有什么关系.相等.
11.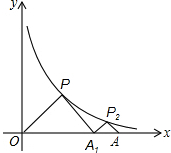 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (2,0) | D. | (2$\sqrt{2}$,0) |
 如图,是反比例函数y=$\frac{6}{x}$和y=$\frac{4}{x}$在第一象限的图象,点P是函数y=$\frac{6}{x}$图象上的一点,过点P作PA∥x轴,PB∥y轴,并分别交函数y=$\frac{4}{x}$的图象于A,B两点,则四边形OAPB的面积为( )
如图,是反比例函数y=$\frac{6}{x}$和y=$\frac{4}{x}$在第一象限的图象,点P是函数y=$\frac{6}{x}$图象上的一点,过点P作PA∥x轴,PB∥y轴,并分别交函数y=$\frac{4}{x}$的图象于A,B两点,则四边形OAPB的面积为( )
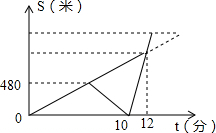 小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.
小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.