题目内容
4.下列从左到右的变形:①$\frac{a}{b}$=$\frac{{a}^{2}}{ab}$;②$\frac{a}{b}$=$\frac{ab}{{b}^{2}}$;③$\frac{a}{b}$=$\frac{ac}{bc}$;④$\frac{a}{b}$=$\frac{a({x}^{2}+1)}{b({x}^{2}+1)}$.其中,正确的是( )| A. | ①② | B. | ②④ | C. | ③④ | D. | ①②③④ |
分析 根据分式的基本性质进行计算并作出正确的判断.
解答 解:①$\frac{a}{b}$=$\frac{{a}^{2}}{ab}$,当a=0时,该等式不成立,故①错误;
②$\frac{a}{b}$=$\frac{ab}{{b}^{2}}$,分式$\frac{a}{b}$的分子、分母同时乘以b,等式仍成立,即$\frac{a}{b}$=$\frac{ab}{{b}^{2}}$,故②正确;
③$\frac{a}{b}$=$\frac{ac}{bc}$,当c=0时,该等式不成立,故③错误;
④$\frac{a}{b}$=$\frac{a({x}^{2}+1)}{b({x}^{2}+1)}$,因为x2+1≠0,即分式$\frac{a}{b}$的分子、分母同时乘以(x2+1),等式仍成立,即$\frac{a}{b}$=$\frac{a({x}^{2}+1)}{b({x}^{2}+1)}$成立,故④正确;
综上所述,正确的②④.
故选:B.
点评 本题考查了分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
15. 如图,下列各式能够表示图中阴影部分的面积的是( )
如图,下列各式能够表示图中阴影部分的面积的是( )
①at+(b-t)t;
②at+bt-t2;
③ab-(a-t)(b-t);
④(a-t)t+(b-t)t+t2.
 如图,下列各式能够表示图中阴影部分的面积的是( )
如图,下列各式能够表示图中阴影部分的面积的是( )①at+(b-t)t;
②at+bt-t2;
③ab-(a-t)(b-t);
④(a-t)t+(b-t)t+t2.
| A. | 只有① | B. | ①② | C. | ①②③ | D. | ①②③④ |
9. 如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2$\sqrt{3}$+2,则∠BAD的度数等于( )
如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2$\sqrt{3}$+2,则∠BAD的度数等于( )
 如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2$\sqrt{3}$+2,则∠BAD的度数等于( )
如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2$\sqrt{3}$+2,则∠BAD的度数等于( )| A. | 120° | B. | 135° | C. | 150° | D. | 以上都不对 |
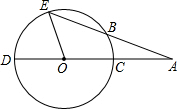 CD是⊙O的直径,AE交⊙O于点B,且AB=OC,∠A=25°,求∠EOD的度数.
CD是⊙O的直径,AE交⊙O于点B,且AB=OC,∠A=25°,求∠EOD的度数.