题目内容
13.已知α为锐角,若4sin2(α-20°)-2($\sqrt{2}$+1)sin(α-20°)+$\sqrt{2}$=0,求α.分析 把等式看作关于sin(α-20°)的一元二次方程,利用因式分解法解得sin(α-20°)=$\frac{1}{2}$或sin(α-20°)=$\frac{\sqrt{2}}{2}$,则利用特殊角的三角函数值得到α-20°=30°或α-20°=45°,然后解关于α的一次方程即可.
解答 解:[2sin(α-20°)-1][2sin(α-20°)-$\sqrt{2}$]=0,
2sin(α-20°)-1=0或2sin(α-20°)-$\sqrt{2}$=0,
所以sin(α-20°)=$\frac{1}{2}$或sin(α-20°)=$\frac{\sqrt{2}}{2}$,
所以α-20°=30°或α-20°=45°,
所以α=50°或65°.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了特殊角的三角函数值.

练习册系列答案
相关题目
7. 如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
 如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )| A. | 50° | B. | 65° | C. | 80° | D. | 100° |
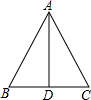 如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=∠2BAD;④S△ABD=S△ACD.其中正确的有( )
如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=∠2BAD;④S△ABD=S△ACD.其中正确的有( )