题目内容
16.已知△ABC的面积为100,它的内切圆半径为5,则△ABC的周长为40.分析 连OA,OB,OC.把三角形ABC分成三个三角形,用三个三角形的面积和表示三角形ABC面积,即可得出△ABC的周长.
解答 解:如图,⊙O是△ABC的内切圆,切点分别为D,E,F.
连OA,OB,OC,OD,OE,OF.
则OD⊥AB,OE⊥BC,OF⊥AC,且OE=OF=OD=5,
∴S△ABC=S△AOB+S△OBC+S△OAC
=$\frac{1}{2}$×5×AB+$\frac{1}{2}$×5×BC+$\frac{1}{2}$×5×AC
=$\frac{5}{2}$(AB+AC+BC)=100,
解得:AB+AC+BC=40.
故答案为:40.
点评 掌握三角形的内切圆的性质、切线的性质、三角形面积的计算方法;根据题意得出三角形的面积=三角形的周长与内切圆半径乘积的一半是解决问题的关键.

练习册系列答案
相关题目
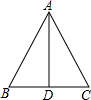 如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=∠2BAD;④S△ABD=S△ACD.其中正确的有( )
如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=∠2BAD;④S△ABD=S△ACD.其中正确的有( )