题目内容
1.某公司准备销售甲、乙两种材料中的一种,设年销售量为x(单位:吨)(x≤6),若销售甲种材料,每吨成本为10万元,每吨售价y(单位:万元)与x的函数关系是:y=-x+30,设年利润为W甲(单位:万元)(年利润=销售额-成本);若销售乙种材料销售利润S与x的函数关系是:S=-2x2+20x,同时每吨可获返利a万元(1≤a≤10),设年利润为W乙(单位:万元)(年利润=销售利润+返利).(1)当x=4时,W甲=64;
(2)当x=4,a=3时,W乙=60;
(3)求W甲与x的函数关系式,并求出x为何值时W甲最大,最大值是多少?
(4)当x=5时,公司想要获得更多的年利润,通过计算说明应选择销售哪种材料?
拓展应用:
现公司决定销售甲种材料,并通过广告宣传提高销售,若一次性投入m(万元)(m>0)的广告费,则年销售量可提高$\frac{1}{4}$m吨(提高后的销售量可突破6吨),此时的年利润为R(单位:万元),当m的值分别为4,8,10时,年利润的最大值分别记为R4、R8、R10,直接写出它们的大小关系:R4<R8<R10.
分析 (1)根据题意即可得到结论;
(2)代入数据计算即可;
(3)由题意得到W甲=x(-x+30)-10x=-x2+20x;根据二次函数的性质即可得到结论;
(4)根据二次函数的性质即可得到结论.
解答 解:(1)W甲=(-4+30-10)×4=64;
(2)W乙=S+4a=-2×42+20×4+4×3=60;
故答案为:64,60;
(3)由题意得:W甲=x(-x+30)-10x=-x2+20x;
所以W甲与x的函数关系式为:W甲=-x2+20x;
∵W甲=-x2+20x=-(x-10)2+100,
∵W甲是x的二次函数,a=-1<0,
∴当x≤6时,W甲随x的增大而增大,
∴当x=6时,W甲最大,最大值=-62+20×6=84;
(4)由题意可得:W乙=-2x2+20x+ax=-2x2+(20+a)x.
当x=5时,W甲=75,W乙=50+5a,
当75>50+5a,即a<5时,W甲>W,所以当1≤a<5时,选择销售甲种材料;
当75=50+5a,即a=5时,W甲=W乙,所以当a=5时,销售甲、乙均可;
当75<50+5a,即a>5时,W甲=W乙,所以当<a≤10时,选择销售乙种材料;
拓展应用:∵R=(-x+30-10)($\frac{1}{4}$m+x)-m=-x2+(20-$\frac{1}{4}$m)x+4m,
∵m的值分别为4,8,10,
R4的最大值=$\frac{215}{2}$,R8的最大值=113,R10=$\frac{1385}{4}$,
∴R4<R8<R10.
故答案为:R4<R8<R10.
点评 此题考查的是二次函数应用能力,建立二次函数的模型,根据二次函数的性质解题是关键.

练习册系列答案
相关题目
16.农民购买农机设备政府会给予一定额度的补贴,其中购买Ⅰ、Ⅱ型农机设备的金额与政府补贴的金额存在表所示的函数对应关系:
(1)分别求出y1和y2的函数解析式;
(2)张大伯打算共用10万元购买Ⅰ、Ⅱ两型农机设备.请你帮助张大伯设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
| 型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
| 购买金额x(万元) | x | 1 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx(k≠0) | 0.4 | y2=ax2+bx(a≠0) | 2.4 | 3.2 |
(2)张大伯打算共用10万元购买Ⅰ、Ⅱ两型农机设备.请你帮助张大伯设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
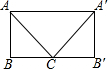
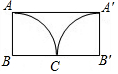
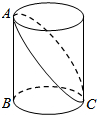 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )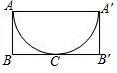
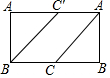
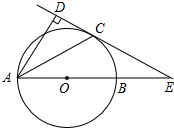 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.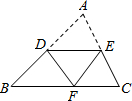 如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为48cm2.
如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为48cm2.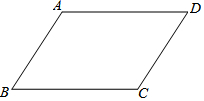 如图,在平行四边形ABCD中,AB<BC.
如图,在平行四边形ABCD中,AB<BC.