题目内容
8.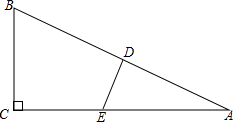 如图所示,在△ABC中,∠C=90°,∠A=30°,DE⊥AB,交AB于D,交AC于E,且CE=DE,那么DE是AB的垂直平分线吗?如果是,请加以证明;如果不是,请说明理由.
如图所示,在△ABC中,∠C=90°,∠A=30°,DE⊥AB,交AB于D,交AC于E,且CE=DE,那么DE是AB的垂直平分线吗?如果是,请加以证明;如果不是,请说明理由.
分析 连接BE,由直角三角形的性质得出∠ABC的度数,根据DE⊥AB,CE=DE可得出BE是∠ABC的平分线,由此可得出结论.
解答  解:是.
解:是.
理由:连接BE,
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=60°.
∵DE⊥AB,CE=DE,
∴BE是∠ABC的平分线,
∴∠DBE=$\frac{1}{2}$∠ABC=30°,
∴∠DBE=∠A,
∴BE=AE,即DE是AB的垂直平分线.
点评 本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
18.下列各组数中,互为相反数的是( )
| A. | 2和$\frac{1}{2}$ | B. | -2和$\frac{1}{2}$ | C. | 2$\frac{3}{8}$和-2.375 | D. | +(-2)和-2 |
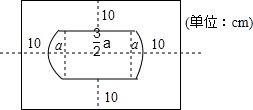 一张餐桌形状如图所示,桌面是由一个长方形和两个半圆组成,一块桌布铺在桌面上,要求桌布垂下部分的宽度都是10cm.
一张餐桌形状如图所示,桌面是由一个长方形和两个半圆组成,一块桌布铺在桌面上,要求桌布垂下部分的宽度都是10cm. 如图,画出△ABC的角平分线AD、中线AE、高AF,并指出AF都是哪些三角形的高.(画对一种线得2分,指对一个三角形的高得1分)
如图,画出△ABC的角平分线AD、中线AE、高AF,并指出AF都是哪些三角形的高.(画对一种线得2分,指对一个三角形的高得1分)
 如图,在△ABC中,∠B=90°,∠BAC=∠C,ED⊥AC于点D,且DE=BE,求∠AED的度数.
如图,在△ABC中,∠B=90°,∠BAC=∠C,ED⊥AC于点D,且DE=BE,求∠AED的度数.