题目内容
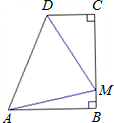 如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则
如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则| CD |
| AB |
考点:直角梯形,全等三角形的判定与性质,等边三角形的性质,勾股定理
专题:
分析:首先过点D作DH⊥AB于H,易得四边形DHBC是矩形,即可得DH=BC=AB,BH=DC,然后设CD=x,AB=BC=DH=y,CM=z,在Rt△CDM,Rt△ABM,Rt△ADH中,由勾股定理可得方程组:x2+z2=y2+(y-z)2,y2+(y-z)2=y2+(y-x)2,即可得x2=2y2-2yx,然后方程两边同除以y2,即可得方程(
)2+
-2=0,解此方程即可求得
的值.
| x |
| y |
| 2x |
| y |
| CD |
| AB |
解答: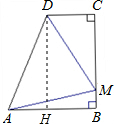 解:过点D作DH⊥AB于H,
解:过点D作DH⊥AB于H,
则∠DHA=90°,
∵∠B=∠C=90°
∴四边形DHBC是矩形,
∴DH=BC,BH=DC,
∵BC=AB,
∴DH=BC=AB,
设CD=x,AB=BC=DH=y,CM=z,
在Rt△CDM,Rt△ABM,Rt△ADH中,
DM2=CD2+CM2,①
AM2=AB2+BM2,②
AD2=AH2+DH2,③
当DM=AM=AD时,△AMD为等边三角形,
则CD2+CM2=AB2+BM2,
AB2+BM2=AH2+DH2,
即x2+z2=y2+(y-z)2④,
y2+(y-z)2=y2+(y-x)2⑤,
化简④得:x2=2y2-2yz,
化简⑤得:x=z,
∴x2=2y2-2yx,
即(
)2+
-2=0,
解得:
=
-1,
=-
-1(舍去).
故
的值为
-1.
 解:过点D作DH⊥AB于H,
解:过点D作DH⊥AB于H,则∠DHA=90°,
∵∠B=∠C=90°
∴四边形DHBC是矩形,
∴DH=BC,BH=DC,
∵BC=AB,
∴DH=BC=AB,
设CD=x,AB=BC=DH=y,CM=z,
在Rt△CDM,Rt△ABM,Rt△ADH中,
DM2=CD2+CM2,①
AM2=AB2+BM2,②
AD2=AH2+DH2,③
当DM=AM=AD时,△AMD为等边三角形,
则CD2+CM2=AB2+BM2,
AB2+BM2=AH2+DH2,
即x2+z2=y2+(y-z)2④,
y2+(y-z)2=y2+(y-x)2⑤,
化简④得:x2=2y2-2yz,
化简⑤得:x=z,
∴x2=2y2-2yx,
即(
| x |
| y |
| 2x |
| y |
解得:
| x |
| y |
| 3 |
| x |
| y |
| 3 |
故
| CD |
| AB |
| 3 |
点评:此题考查了直角梯形的性质、勾股定理、等边三角形的性质以及方程组的应用.此题难度较大,解题的关键是作出辅助线,利用勾股定理得方程组,化简求得(
)2+
-2=0是解此题的关键.
| x |
| y |
| 2x |
| y |

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠AOC=116°,则∠D的读数为( )
如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠AOC=116°,则∠D的读数为( )| A、64° | B、58° |
| C、32° | D、29° |
两圆的直径分别为4和6,圆心距为10,则两圆的位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
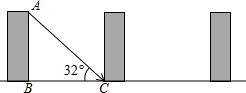 为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.
为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.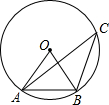 如图,A、B、C三点在⊙O上,∠C=30°,则△OAB是
如图,A、B、C三点在⊙O上,∠C=30°,则△OAB是 为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.
为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.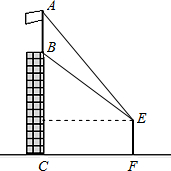 如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的观测点E与地面的距离EF为1.6m.
如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的观测点E与地面的距离EF为1.6m.