题目内容
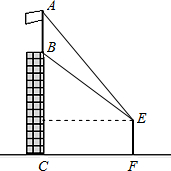 如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的观测点E与地面的距离EF为1.6m.
如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的观测点E与地面的距离EF为1.6m.(1)求建筑物BC的高度;
(2)求旗杆AB的高度.
(注:结果精确到0.1m,参考数据:
| 2 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:压轴题
分析:(1)先过点E作ED⊥BC于D,由已知底部B的仰角为45°得BD=ED=FC=12m,DC=EF=1.6m,从而求出BC.
(2)由已知由E点观测到旗杆顶部A的仰角为60°可求出AD,则AB=AD-BD.
(2)由已知由E点观测到旗杆顶部A的仰角为60°可求出AD,则AB=AD-BD.
解答: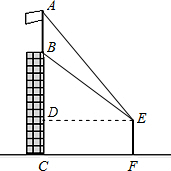 解:(1)过点E作ED⊥BC于D,
解:(1)过点E作ED⊥BC于D,
则四边形DCFE是矩形,
∴DE=CF=12m,EF=CD=1.6m,
根据题意得:∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=12m,
∴BC=BD+DC=BD+EF=12+1.6=13.6(m),
答:建筑物BC的高度为13.6m.
(2)由题意得:∠AED=60°,
∴AD=ED•tan60°=12×
≈12×1.73≈20.8(m),
∴AB=AD-BD=20.8-12=38.8(m).
答:旗杆AB的高度约为8.8m.
 解:(1)过点E作ED⊥BC于D,
解:(1)过点E作ED⊥BC于D,则四边形DCFE是矩形,
∴DE=CF=12m,EF=CD=1.6m,
根据题意得:∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=12m,
∴BC=BD+DC=BD+EF=12+1.6=13.6(m),
答:建筑物BC的高度为13.6m.
(2)由题意得:∠AED=60°,
∴AD=ED•tan60°=12×
| 3 |
∴AB=AD-BD=20.8-12=38.8(m).
答:旗杆AB的高度约为8.8m.
点评:此题考查了仰角的应用.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
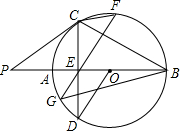 已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于
| 1 |
| 2 |
| A、①②④ | B、③④ |
| C、①②③ | D、①②③④ |
一个圆锥的侧面积是底面积的3倍,则这个圆锥的侧面展开图的圆心角的度数为( )
| A、180° | B、120° |
| C、90° | D、60° |
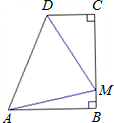 如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则
如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则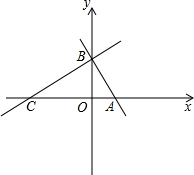 如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB-
如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB- 如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=30°,则∠D的度数为
如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=30°,则∠D的度数为 如图是反比例函数
如图是反比例函数