题目内容
如图是某中学生公寓时的一个示意图(每栋公寓均朝正南方向,且楼高相等,相邻两栋公寓的距离也相等).已知该地区冬季正午的阳光与水平线的夹角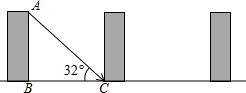 为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.
为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.
(1)若设计公寓高为20米,则相邻两公寓之间的距离至少需要多少米时,采光不受影响?
(2)该中学现已建成的公寓为5层,每层高为3米,相邻两公寓的距离24米,问其采光是否符合要求?
(参考数据:取sin32°=
,cos32°=
,tan32°=
)
 为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.
为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.(1)若设计公寓高为20米,则相邻两公寓之间的距离至少需要多少米时,采光不受影响?
(2)该中学现已建成的公寓为5层,每层高为3米,相邻两公寓的距离24米,问其采光是否符合要求?
(参考数据:取sin32°=
| 53 |
| 100 |
| 106 |
| 125 |
| 5 |
| 8 |
考点:解直角三角形的应用
专题:
分析:(1)在直角三角形ABC中,已知AB利用锐角三角函数求得BC的长即可;
(2)利用楼高求得不受影响时候两楼之间的距离与24米比较即可得到结果;
(2)利用楼高求得不受影响时候两楼之间的距离与24米比较即可得到结果;
解答:解:(1)∵在直角三角形ABC中,AB=20米,∠ACB=32°,
∴
=tan32°
∴BC=
=
=32米,
∴相邻两公寓之间的距离至少需要32米时,采光不受影响;
(2)∵楼高=3×5=15米,
∴不受影响时两楼之间的距离为15÷tan32°=24米,
∵相邻两公寓的距离恰为24米,
∴符合采光要求;
∴
| AB |
| BC |
∴BC=
| AB |
| tan32° |
| 20 | ||
|
∴相邻两公寓之间的距离至少需要32米时,采光不受影响;
(2)∵楼高=3×5=15米,
∴不受影响时两楼之间的距离为15÷tan32°=24米,
∵相邻两公寓的距离恰为24米,
∴符合采光要求;
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
相关题目
如果分式方程
=
-1有增根,那么常数m的值为( )
| x+5 |
| x-3 |
| m-1 |
| x-3 |
| A、3 | B、-5 | C、8 | D、9 |
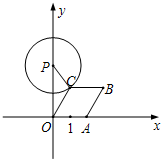 如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t= 如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数
如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数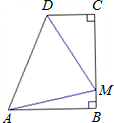 如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则
如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则