题目内容
 如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果BE:BC=2:3,那么下列各式错误的是( )
如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果BE:BC=2:3,那么下列各式错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:结合平行四边形的性质及平行线分线段成比例逐项判断即可.
解答:解:∵BE:BC=2:3,
∴
=
=2,故A正确;
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∴
=
=
,故B正确;
∵AD∥BE,
∴
=
=
=
,故C不正确;
∴
=
=
=
,故D正确;
故选C.
∴
| BE |
| EC |
| 2 |
| 1 |
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∴
| EC |
| AD |
| EC |
| BC |
| 1 |
| 3 |
∵AD∥BE,
∴
| EF |
| AF |
| BE |
| AD |
| BE |
| BC |
| 2 |
| 3 |
∴
| BF |
| DF |
| BE |
| AD |
| BE |
| BC |
| 2 |
| 3 |
故选C.
点评:本题主要考查平行四边形的性质及平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.

练习册系列答案
相关题目
抛物线y=-2x2-4x-5经过平移得到y=-2x2,平移方法是( )
| A、向左平移1个单位,再向下平移3个单位 |
| B、向左平移1个单位,再向上平移3个单位 |
| C、向右平移1个单位,再向下平移3个单位 |
| D、向右平移1个单位,再向上平移3个单位 |
若A(-3.5,y1),B(-1,y2),C(1,y2)为二次函数y=-x2-4x+5的图象上的三点,则y1,y2,y3的大小关系是( )
| A、y1<y2<y3 |
| B、y2<y3<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
 已知在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5);
已知在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5);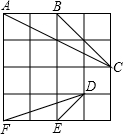 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.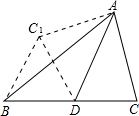 如图,AD是△ABC的中线,∠ADC=60°,△ADC沿直线AD解析,点C落在点C1的位置,如果DC=2,那么BC1的值为( )
如图,AD是△ABC的中线,∠ADC=60°,△ADC沿直线AD解析,点C落在点C1的位置,如果DC=2,那么BC1的值为( )