题目内容
 已知在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5);
已知在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5);(1)求这个二次函数的解析式;
(2)将这个二次函数的图象向上平移,交y轴于点C,其纵坐标为m,请用m的代数式表示平移后函数图象顶点M的坐标;
(3)在第(2)小题的条件下,如果点P的坐标为(2,3),CM平分∠PCO,求m的值.
考点:二次函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)根据顶点坐标公式,可得顶点坐标,根据图象的平移,可得M点的坐标;
(3)根据角平分线的性质,可得全等三角形,根据全等三角形的性质,可得方程组,根据解方程组,可得答案.
(2)根据顶点坐标公式,可得顶点坐标,根据图象的平移,可得M点的坐标;
(3)根据角平分线的性质,可得全等三角形,根据全等三角形的性质,可得方程组,根据解方程组,可得答案.
解答:解:(1)由二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5),得
,解得
.
二次函数的解析式y=x2-4x;
(2)y=x2-4x的顶点M坐标(2,-4),
这个二次函数的图象向上平移,交y轴于点C,其纵坐标为m,
顶点M坐标向上平移m,即M(2,m-4);
(3)由待定系数法,得CP的解析式为y=
x+m,
如图:
作MG⊥PC于G,设G(a,
a+m).
由角平分线上的点到角两边的距离相等,
DM=MG.
在Rt△DCM和Rt△GCM中
,
Rt△DCM≌Rt△GCM(HL).
CG=DC=4,MG=DM=2,
,
化简,得8m=36,
解得m=
.
|
|
二次函数的解析式y=x2-4x;
(2)y=x2-4x的顶点M坐标(2,-4),
这个二次函数的图象向上平移,交y轴于点C,其纵坐标为m,
顶点M坐标向上平移m,即M(2,m-4);
(3)由待定系数法,得CP的解析式为y=
| 3-m |
| 2 |
如图:

作MG⊥PC于G,设G(a,
| 3-m |
| 2 |
由角平分线上的点到角两边的距离相等,
DM=MG.
在Rt△DCM和Rt△GCM中
|
Rt△DCM≌Rt△GCM(HL).
CG=DC=4,MG=DM=2,
|
化简,得8m=36,
解得m=
| 9 |
| 2 |
点评:本题考察了二次函数综合题,(1)利用了待定系数法求函数解析式,(2)利用了二次函数顶点坐标公式,图象的平移方法;(3)利用了角平分线的性质,全等三角形的性质.

练习册系列答案
相关题目
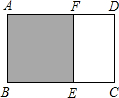 已知矩形纸片ABCD中,AB=1,如图,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为( )
已知矩形纸片ABCD中,AB=1,如图,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果BE:BC=2:3,那么下列各式错误的是( )
如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果BE:BC=2:3,那么下列各式错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
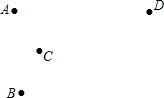 A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)
A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)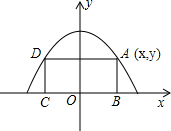 已知:如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,矩形ABCD在抛物线与x轴所围成的图形内.
已知:如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,矩形ABCD在抛物线与x轴所围成的图形内.