题目内容
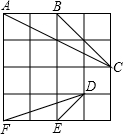 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=
(2)判断△ABC与△DEF是否相似,并说明理由.
(3)请在图中再画出一个和△ABC相似,但与图中三角形均不全等的格点三角形.
考点:作图—相似变换
专题:网格型
分析:(1)利用图形结合正方形的性质以及勾股定理得出即可;
(2)利用相似三角形的判定方法得出即可;
(3)将三角形的三边变为原来的
,进而得出答案.
(2)利用相似三角形的判定方法得出即可;
(3)将三角形的三边变为原来的
| 1 |
| 2 |
解答: 解:(1)由题意可得:∠ABC=90°+45°=135°,
解:(1)由题意可得:∠ABC=90°+45°=135°,
BC=2
;
故答案为:135°,2
;
(2)相似,
理由:∵AB=2BC=2
,AC=2
,DE=
,EF=2,DF=
,
∴
=
=
=
,
∴△ABC∽△DEF;
(3)如图所示:△A′B′C′.
 解:(1)由题意可得:∠ABC=90°+45°=135°,
解:(1)由题意可得:∠ABC=90°+45°=135°,BC=2
| 2 |
故答案为:135°,2
| 2 |
(2)相似,
理由:∵AB=2BC=2
| 2 |
| 5 |
| 2 |
| 10 |
∴
| AB |
| DE |
| BC |
| EF |
| AC |
| DF |
| 2 |
∴△ABC∽△DEF;
(3)如图所示:△A′B′C′.
点评:此题主要考查了相似三角形的判定与性质,正确结合网格求出答案是解题关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
在-6,2.8,-
,48,0,-6.6,-6π,2.020020002…,
中,无理数有( )
| 1 |
| 2 |
| 22 |
| 7 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果BE:BC=2:3,那么下列各式错误的是( )
如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果BE:BC=2:3,那么下列各式错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,点B位于点O的南偏西45°方向上,∠AOB=70°,则点A位于O的( )
如图,点B位于点O的南偏西45°方向上,∠AOB=70°,则点A位于O的( )| A、北偏西65° |
| B、西偏北35° |
| C、南偏北25° |
| D、东偏北45° |
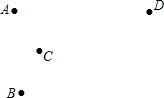 A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)
A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)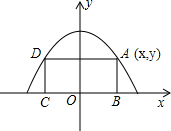 已知:如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,矩形ABCD在抛物线与x轴所围成的图形内.
已知:如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,矩形ABCD在抛物线与x轴所围成的图形内.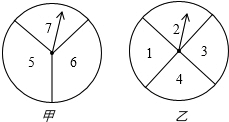 如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.
如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.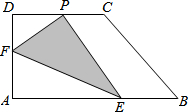 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.AE=5,P落在线段CD上时,PD=
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.AE=5,P落在线段CD上时,PD=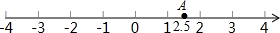 如图,在数轴上画出表示3.5的相反数的点B,再把点A向左移动1.5个单位,得到点C.
如图,在数轴上画出表示3.5的相反数的点B,再把点A向左移动1.5个单位,得到点C.