题目内容
3.如图,一组抛物线的顶点A1(x1,y1),A2(x2,y2),…An(xn,yn)(n为正整数)依次是反比例函数y=$\frac{9}{x}$ 图象上的点,第一条抛物线以A1(x1,y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2,y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn,yn)为顶点且经过点Bn-1(2n-2,0),B2n(2n,0),等腰△AnBn-1Bn为第n个三角形.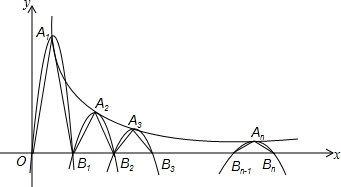
(1)请直接写出A3的坐标(5,$\frac{9}{5}$);并求出第一个抛物线的解析式
(2)请直接写出An的坐标(2n-1,$\frac{9}{2n-1}$),并求出第几个三角形的面积为整数?
(3)①若第m个三角形和第n个三角形顶角互补,直接写出m,n(m>n)的值.
②若第n条抛物线为y=anx2+bnx+cn满足bn+cn=2an,直接写出n的值.
分析 (1)根据抛物线的对称性和反比例函数图象上点的坐标特征易求得到A1(1,9),A2(3,3),A3(5,$\frac{9}{5}$),则设第一个抛物线解析式为y=a(x-1)2+9,把O(0,0)代入该函数解析式即可求得a的值;
(2)根据(1)的规律即可得出An的坐标;根据抛物线与x轴的两个交点坐标可以求得每一个等腰三角形的底边长;由反比例函数图象上点的坐标特征,可以得到该底上的高线,然后利用三角形的面积公式得到第n个等腰三角形的面积公式,然后取整即可;
(3)①根据作第m个三角形和第n个三角形底边上的高AmC和AnD,构建相似三角形△AmCBm-1∽△AnDBn-1,利用相似三角形的对应边成比例来求m、n的值.注意m、n都是正整数.
②设第n条抛物线的解析式为顶点式:y=an(x-2n+1)2+$\frac{9}{2n-1}$.把点(2n,0)代入函数解析式得到:an=-$\frac{9}{2n-1}$.利用换元思想将该解析式转化为y=-m(x-2n+1)2+m=-mx2+m(4n-2)x-m(2n-1)2+m.则结合已知条件可以推知4n-2-(2n-1)2+1=-2由此可以求得n的值.
解答 解:(1)∵第一条抛物线过点O(0,0),B1(2,0),
∴该抛物线的对称轴是x=1.
又∵顶点A1(x1,y1)在反比例函数y=$\frac{9}{x}$图象上,
∴y1=9,
即第一条抛物线的顶点坐标是A1(1,9),
第二条抛物线的顶点坐标是A2(3,3),
第三条抛物线的顶点坐标是A3(5,$\frac{9}{5}$),.
设第一个抛物线为y=a(x-1)2+9(a≠0),
把点O(0,0)代入,得到:0=a+9,
解得 a=-9.
所以第一条抛物线的解析式是y=-9(x-1)2+9;
(2)由(1)的规律可知An (2n-1,$\frac{9}{2n-1}$);
∵第一个等腰三角形的底边长为:2,高长为:$\frac{9}{\frac{2+0}{2}}$=$\frac{9}{1}$,面积为:$\frac{1}{2}$×2×$\frac{9}{1}$=$\frac{9}{2×1-1}$;
第一个等腰三角形的底边长为:2,高长为:$\frac{9}{\frac{4+2}{2}}$=$\frac{9}{3}$,面积为:$\frac{1}{2}$×2×$\frac{9}{3}$=$\frac{9}{2×2-1}$;
第一个等腰三角形的底边长为:2,高长为:$\frac{9}{\frac{6+4}{2}}$=$\frac{9}{5}$,面积为:$\frac{1}{2}$×2×$\frac{9}{5}$=$\frac{9}{2×3-1}$;
…
第n等腰三角形的底边长为:2,高长为:$\frac{9}{2n-1}$,面积为:$\frac{1}{2}$×2×$\frac{9}{2n-1}$=$\frac{9}{2n-1}$;
即第n个三角形的面积是$\frac{9}{2n-1}$.
当n=1,2,5时为整数;
(3)①作第m个三角形和第n个三角形底边上的高AmC和AnD,
∵顶角互补,
∴底角互余.
即△AmCBm-1∽△AnDBn-1,
∴$\frac{1}{\frac{9}{2n-1}}$=$\frac{9}{\frac{2m-1}{1}}$,即(2m-1)(2n-1)=81,
∵m、n都是正整数,
∴$\left\{\begin{array}{l}{m=41}\\{n=1}\end{array}\right.$或$\left\{\begin{array}{l}{m=14}\\{n=2}\end{array}\right.$.
②设第n条抛物线的解析式为y=an(x-2n+1)2+$\frac{9}{2n-1}$.
又∵过点(2n,0),
∴an=-$\frac{9}{2n-1}$.
设$\frac{9}{2n-1}$=m,
∴y=-m(x-2n+1)2+m=-mx2+m(4n-2)x-m(2n-1)2+m.
∵第n条抛物线为y=anx2+bnx+cn满足bn+cn=2an,
∴m(4n-2)-m(2n-1)2+m=-2m,
4n-2-(2n-1)2+1=-2,n=2.
点评 本题综合考查了待定系数法求二次函数解析式,反比例函数图象上点的坐标特征以及相似三角形的判定与性质.整个解题过程,利用抛物线的对称轴和反比例函数图象上的坐标特征来求相关点的坐标和相关线段的长度是解题的关键,此题综合性强,有一定的难度.

| A. | 3 | B. | 4 | C. | 5 | D. | 4或5 |
 某银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).下面是这次调查统计得到的频数分布表和频数分布直方图.
某银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).下面是这次调查统计得到的频数分布表和频数分布直方图.| 分组 | 频数 | 频率 | |
| 一组 | 0<t≤5 | 10 | 0.1 |
| 二组 | 5<t≤10 | 30 | 0.3 |
| 三组 | 10<t≤15 | 25 | 0.25 |
| 四组 | 15<t≤20 | 20 | 0.2 |
| 五组 | 20<t≤25 | 15 | 0.15 |
| 合计 | 1.00 | ||
(2)补全频数分布直方图;
(3)据调查顾客对服务质量的满意程度与所用时间t的关系如下:
| 所用时间t | 顾客满意程度 |
| 0<t≤10 | 比较满意 |
| 10<t≤15 | 基本满意 |
| t>15 | 比较差 |
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
 如图,点B在线段AE上,∠1=∠2,如果添加一个条件,即可得到△ABC≌△ABD,那么这个条件可以是AC=AD或∠ABC=∠ABD或∠C=∠D(要求:不在图中添加其他辅助线,写出一个条件即可)
如图,点B在线段AE上,∠1=∠2,如果添加一个条件,即可得到△ABC≌△ABD,那么这个条件可以是AC=AD或∠ABC=∠ABD或∠C=∠D(要求:不在图中添加其他辅助线,写出一个条件即可)
 如图,在平面直角坐标系xOy中,矩形ABCD各边都平行于坐标轴,且A(-2,2),C(3,-2).对矩形ABCD及其内部的点进行如下操作:把每个点的横坐标乘以a,纵坐标乘以b,将得到的点再向右平移k(k>0)个单位,得到矩形A′B′C′D′及其内部的点(A′B′C′D′分别与ABCD对应).E(2,1)经过上述操作后的对应点记为E′.
如图,在平面直角坐标系xOy中,矩形ABCD各边都平行于坐标轴,且A(-2,2),C(3,-2).对矩形ABCD及其内部的点进行如下操作:把每个点的横坐标乘以a,纵坐标乘以b,将得到的点再向右平移k(k>0)个单位,得到矩形A′B′C′D′及其内部的点(A′B′C′D′分别与ABCD对应).E(2,1)经过上述操作后的对应点记为E′.