方程组$\left\{\begin{array}{l}{x-y=0}\\{x+y=2}\end{array}\right.$的解为( )A．$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$B．$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$C．$\left\{\be 题目和参考答案——青夏教育精英家教网—

题目内容

18．方程组$\left\{\begin{array}{l}{x-y=0}\\{x+y=2}\end{array}\right.$的解为（　　）

A．

$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$

B．

$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$

C．

$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$

D．

$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$

分析方程组利用加减消元法求出解即可．

解答解：$\left\{\begin{array}{l}{x-y=0①}\\{x+y=2②}\end{array}\right.$，
①+②得：2x=2，即x=1，
①-②得：-2y=-2，即y=1，
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，
故选D

点评此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

8．

如图是正方体的一种展开图，其中每个面上都有一个数字，那么在原正方体中，与数字6相对面上的数字是（　　）

9．

如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且∠D=2∠CAD．若CD=2，则BD的长为2$\sqrt{2}$-2．

6．有3张扑克牌，分别是红桃3、红桃4和黑桃5，把牌洗匀后先抽取一张，记下颜色和数字后将牌放回，洗匀后再抽取一张，则两次抽得相同颜色的概率是多少？

13．已知a，b是关于x的方程x²-（2k+1）x+k（k+1）=0的两个实数根，则a+b+ab的最小值是-$\frac{5}{4}$．

3．如图，一组抛物线的顶点A₁（x₁，y₁），A₂（x₂，y₂），…A_n（x_n，y_n）（n为正整数）依次是反比例函数y=$\frac{9}{x}$ 图象上的点，第一条抛物线以A₁（x₁，y₁）为顶点且过点O（0，0），B₁（2，0），等腰△A₁OB₁为第一个三角形；第二条抛物线以A₂（x₂，y₂）为顶点且经过点B₁（2，0），B₂（4，0），等腰△A₂B₁B₂为第二个三角形；…；第n条抛物线以A_n（x_n，y_n）为顶点且经过点B_n-1（2n-2，0），B_2n（2n，0），等腰△A_nB_n-1B_n为第n个三角形．

（1）请直接写出A₃的坐标（5，$\frac{9}{5}$）；并求出第一个抛物线的解析式
（2）请直接写出A_n的坐标（2n-1，$\frac{9}{2n-1}$），并求出第几个三角形的面积为整数？
（3）①若第m个三角形和第n个三角形顶角互补，直接写出m，n（m＞n）的值．
②若第n条抛物线为y=a_nx²+b_nx+c_n满足b_n+c_n=2a_n，直接写出n的值．

10．

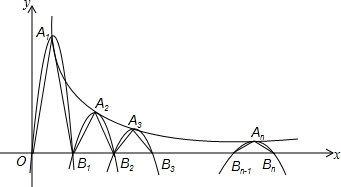
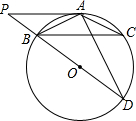如图，⊙O是△ABC 的外接圆，AB=AC，BD是⊙O的直径，PA∥BC，与DB的延长线交于点P，连接AD．
（1）求证：PA是⊙O的切线；
（2）若AB=$\sqrt{5}$，BC=4，求AD的长．

7．

综合实践课上，小宇设计用光学原理来测量公园假山的高度，把一面镜子放在与假山AC距离为21米的B处，然后沿着射线CB退后到点E，这时恰好在镜子里看到山头A，利用皮尺测量BE=2.1米．若小宇的身高是1.7米，则假山AC的高度为17米．

8．

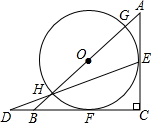如图，在等腰直角三角形△ABC中，∠ACB=90°，以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F，与AB分别交于点G、H，且EH的延长线和CB的延长线交于点D．
（1）求证：AE=CE；
（2）求tan∠DEC的值．

试题分类