题目内容
已知直角坐标平面上的点A(2,6)和B(2,1),反比例函数y=
与线段AB有交点,P是函数图象上的一点,过点P作PQ⊥x轴,Q是垂足,则△OPQ的面积S的取值范围是 .
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:由反比例函数与线段AB有交点可求出k的取值范围,再利用k表示出△OPQ的面积,可得出答案.
解答:解:
当反比例函数过A点时,代入可求得k=12,
当反比例函数过B点时,代入可求得k=2,
∴k的取值范围为:2≤k≤12,
设P点坐标为(x,y),则xy=k(k>0),
∴S=
k,
∴1≤S≤6,
故答案为:1≤S≤6.
当反比例函数过A点时,代入可求得k=12,
当反比例函数过B点时,代入可求得k=2,
∴k的取值范围为:2≤k≤12,
设P点坐标为(x,y),则xy=k(k>0),
∴S=
| 1 |
| 2 |
∴1≤S≤6,
故答案为:1≤S≤6.
点评:本题主要考查反比例函数k的几何意义,根据条件求得k的取值范围是解题的关键.

练习册系列答案
相关题目
下列各数中用科学记数法表示正确的是( )
| A、0.42×105 |
| B、42×103 |
| C、4.2×104 |
| D、4.2×10000 |
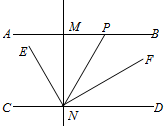 如图,直线AB∥CD,MN⊥AB于M交CD于M交CD于N,P为射线MF上一动点,连接NP,NE平分∠CNP,NF⊥NE,当点P运动时,请你探究
如图,直线AB∥CD,MN⊥AB于M交CD于M交CD于N,P为射线MF上一动点,连接NP,NE平分∠CNP,NF⊥NE,当点P运动时,请你探究
 如图,OC是∠AOB内的一条射线,OM平分∠AOB,ON平分∠BOC.
如图,OC是∠AOB内的一条射线,OM平分∠AOB,ON平分∠BOC.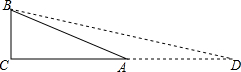 小明是一个非常喜欢动脑筋肯钻研的同学,学习了特殊角的三角函数值后,他进行了如下探究:根据tan30°=
小明是一个非常喜欢动脑筋肯钻研的同学,学习了特殊角的三角函数值后,他进行了如下探究:根据tan30°= 如图,AE平分∠BAC,FD⊥BC.求证:∠EFD=
如图,AE平分∠BAC,FD⊥BC.求证:∠EFD=