题目内容
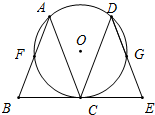 如图,在△ABC中,AB=AC,将△ABC沿BC方向平移得到△DCE,⊙O经过A、C、D三点.
如图,在△ABC中,AB=AC,将△ABC沿BC方向平移得到△DCE,⊙O经过A、C、D三点.(1)求证:BE是⊙O的切线;
(2)若∠ABC=72°,连接CF,判断线段CF与DG的大小.
考点:切线的判定
专题:
分析:(1)如图,作辅助线,证明△AOC≌△DOC,得到∠ACO=∠DCO;证明∠ACB=∠DCE,得到∠OCB=∠OCE=90°,即可解决问题.
(2)证明∠FAC=∠FCA,进而得到AF=CF;由圆的对称性知:AF=DG,即可解决问题.
(2)证明∠FAC=∠FCA,进而得到AF=CF;由圆的对称性知:AF=DG,即可解决问题.
解答: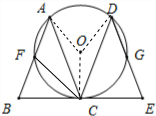 解:(1)连接OA、OC、OD;
解:(1)连接OA、OC、OD;
在△AOC与△DOC中,
,
∴△AOC≌△DOC(SSS),
∴∠ACO=∠DCO;而AB=AC,
∴∠B=∠ACB,∠ACB=∠DCE;
∴∠OCB=∠OCE=
×180°=90°,
∴BE是⊙O的切线.
(2)CF=DG.理由如下:
若∠ABC=72°,则:
∠BCA=180°-2×72°=36°,
∵BC是⊙O的切线,
∴∠BCE=∠FAC=36°;
∠ACF=72°-36°=36°,
∴∠FAC=∠FCA,AF=CF;
由圆的对称性知:AF=DG,
∴CF=DG.
 解:(1)连接OA、OC、OD;
解:(1)连接OA、OC、OD;在△AOC与△DOC中,
|
∴△AOC≌△DOC(SSS),
∴∠ACO=∠DCO;而AB=AC,
∴∠B=∠ACB,∠ACB=∠DCE;
∴∠OCB=∠OCE=
| 1 |
| 2 |
∴BE是⊙O的切线.
(2)CF=DG.理由如下:
若∠ABC=72°,则:
∠BCA=180°-2×72°=36°,
∵BC是⊙O的切线,
∴∠BCE=∠FAC=36°;
∠ACF=72°-36°=36°,
∴∠FAC=∠FCA,AF=CF;
由圆的对称性知:AF=DG,
∴CF=DG.
点评:该题主要考查了圆的切线的判定及其性质的应用问题;解题的关键是作辅助线,运用切线的判定定理及性质定理来分析、判断、推理或解答.

练习册系列答案
相关题目
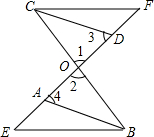 EF与BC交于点O,AB∥CD,OA=OD,AE=DF,∠1、∠2、∠3、∠4如图所示,求证:EB∥CF.
EF与BC交于点O,AB∥CD,OA=OD,AE=DF,∠1、∠2、∠3、∠4如图所示,求证:EB∥CF.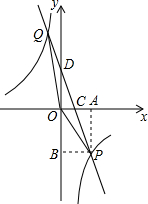 如图,一次函数y=kx+3的图象与反比例函数y=
如图,一次函数y=kx+3的图象与反比例函数y=