题目内容
设一个三角形的三边长是a、b、c.
(1)a2、b2、c2一定可以是一个三角形的边长吗?若是,说明理由;若不是,请举例说明.
(2)ab、bc、ca一定可以是一个三角形的三边长吗?若是,说明理由;若不是,请举例说明.
(3)求证:a2+bc、b2+ca、c2+ab一定可以是一个三角形的三边长.
(1)a2、b2、c2一定可以是一个三角形的边长吗?若是,说明理由;若不是,请举例说明.
(2)ab、bc、ca一定可以是一个三角形的三边长吗?若是,说明理由;若不是,请举例说明.
(3)求证:a2+bc、b2+ca、c2+ab一定可以是一个三角形的三边长.
考点:三角形边角关系
专题:
分析:(1)不一定;举出一个反例:a=3、b=4、c=5即可解决问题.
(2)不一定;举出一个反例:a=2、b=4、c=5即可解决问题.
(3)运用均值不等式a2+b2≥2ab,结合三角形的边角关系,即可解决问题.
(2)不一定;举出一个反例:a=2、b=4、c=5即可解决问题.
(3)运用均值不等式a2+b2≥2ab,结合三角形的边角关系,即可解决问题.
解答:(1)解:a2、b2、c2不一定是一个三角形的边长;
如a=3、b=4、c=5是一个直角三角形的边长,
此时,a2=9,b2=16,c2=25;
∵9+16=25,这与三角形中任意两边之和大于第三边矛盾,
∴a2、b2、c2不是一个三角形的边长.
(2)解:ab、bc、ca不一定是一个三角形的三边长;
如a=2,b=4,c=5是一个三角形的边长,
此时ab=8,bc=20,ac=10;
∵8+10<20,这与三角形中任意两边之和大于第三边矛盾,
∴ab、bc、ca不是一个三角形的三边长.
(3)证明:∵a2+b2≥2ab,
∴a2+bc+b2+ca≥2ab+(a+b)c>ab+(a+b)c,
∵a+b>c,
∴a2+bc+b2+ca>c2+ab;
同理可证:b2+ca+c2+ab>a2+bc,
a2+bc+c2+ab>b2+ca,
∴a2+bc、b2+ca、c2+ab一定可以是一个三角形的三边长.
如a=3、b=4、c=5是一个直角三角形的边长,
此时,a2=9,b2=16,c2=25;
∵9+16=25,这与三角形中任意两边之和大于第三边矛盾,
∴a2、b2、c2不是一个三角形的边长.
(2)解:ab、bc、ca不一定是一个三角形的三边长;
如a=2,b=4,c=5是一个三角形的边长,
此时ab=8,bc=20,ac=10;
∵8+10<20,这与三角形中任意两边之和大于第三边矛盾,
∴ab、bc、ca不是一个三角形的三边长.
(3)证明:∵a2+b2≥2ab,
∴a2+bc+b2+ca≥2ab+(a+b)c>ab+(a+b)c,
∵a+b>c,
∴a2+bc+b2+ca>c2+ab;
同理可证:b2+ca+c2+ab>a2+bc,
a2+bc+c2+ab>b2+ca,
∴a2+bc、b2+ca、c2+ab一定可以是一个三角形的三边长.
点评:该题主要考查了三角形的三边关系及其应用问题;解题的关键是灵活运用三边关系来分析、变形、讨论、判断;对综合的分析问题解决问题的能力、灵活的变形转化能力等均提出了较高的要求.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
下列方程组不是三元一次方程组的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在△ABC中,∠C=90°,BC=2,
=
,则边AC的长是( )
| BC |
| AB |
| 2 |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
当x>2时,|1+
|等于( )
| (x-2)2 |
| A、1-x | B、x-1 |
| C、3-x | D、x-3 |
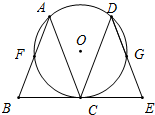 如图,在△ABC中,AB=AC,将△ABC沿BC方向平移得到△DCE,⊙O经过A、C、D三点.
如图,在△ABC中,AB=AC,将△ABC沿BC方向平移得到△DCE,⊙O经过A、C、D三点.