题目内容
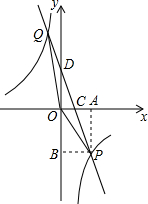 如图,一次函数y=kx+3的图象与反比例函数y=
如图,一次函数y=kx+3的图象与反比例函数y=| m |
| x |
(1)求点D的坐标;
(2)求一次函数与反比例函数的表达式;
(3)求△OPQ的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将x=0代入y=kx+3,求出y的值,即可得到一次函数与y轴的交点D的坐标;
(2)先证明△COD∽△CAP,根据相似三角形对应边的比相等得到
=
=1,由OD=3,求得AP=OB=3,则DB=OD+OB=6,再由S△DBP=6,求出BP=2,于是P(2,-3),然后把P点坐标分别代入y=kx+3与y=
,利用待定系数法即可求解;
(3)先把y=-3x+3代入y=-
,解方程得到Q点坐标,再根据△OPQ的面积=△OPD的面积+△OQD的面积,代入数值计算即可求解.
(2)先证明△COD∽△CAP,根据相似三角形对应边的比相等得到
| OD |
| AP |
| OC |
| AC |
| m |
| x |
(3)先把y=-3x+3代入y=-
| 6 |
| x |
解答:解:(1)∵一次函数y=kx+3与y轴相交于点D,
∴令x=0,解得y=3,
∴D的坐标为(0,3);
(2)∵OD⊥OA,AP⊥OA,
∴∠DOC=∠CAP=90°.
在△COD与△CAP中,
,
∴△COD∽△CAP,
∴
=
=1,OD=3,
∴AP=OB=3,
∴DB=OD+OB=6,
∵S△DBP=6,
∴
×6×BP=6,
∴BP=2,故P(2,-3),
把P点坐标代入y=kx+3,
 得-3=2k+3,解得k=-3,
得-3=2k+3,解得k=-3,
则一次函数的解析式为:y=-3x+3;
把P点坐标代入反比例函数解析式得m=-6,
则反比例解析式为:y=-
;
(3)把y=-3x+3代入y=-
,得-3x+3=-
,
整理,得x2-x-2=0,
解得x=-1或2,
当x=-1时,y=6,
当x=2时,y=-3,
∵P(2,-3),
∴Q(-1,6).
△OPQ的面积=△OPD的面积+△OQD的面积
=
×3×2+
×3×1
=3+1.5
=4.5.
∴令x=0,解得y=3,
∴D的坐标为(0,3);
(2)∵OD⊥OA,AP⊥OA,
∴∠DOC=∠CAP=90°.
在△COD与△CAP中,
|
∴△COD∽△CAP,
∴
| OD |
| AP |
| OC |
| AC |
∴AP=OB=3,
∴DB=OD+OB=6,
∵S△DBP=6,
∴
| 1 |
| 2 |
∴BP=2,故P(2,-3),
把P点坐标代入y=kx+3,
 得-3=2k+3,解得k=-3,
得-3=2k+3,解得k=-3,则一次函数的解析式为:y=-3x+3;
把P点坐标代入反比例函数解析式得m=-6,
则反比例解析式为:y=-
| 6 |
| x |
(3)把y=-3x+3代入y=-
| 6 |
| x |
| 6 |
| x |
整理,得x2-x-2=0,
解得x=-1或2,
当x=-1时,y=6,
当x=2时,y=-3,
∵P(2,-3),
∴Q(-1,6).
△OPQ的面积=△OPD的面积+△OQD的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=3+1.5
=4.5.
点评:本题主要考查了反比例函数和一次函数的交点问题,相似三角形的判定与性质,待定系数法求函数的解析式,三角形的面积,在解题时要注意知识的综合运用与图形相结合是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列方程组不是三元一次方程组的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
当x>2时,|1+
|等于( )
| (x-2)2 |
| A、1-x | B、x-1 |
| C、3-x | D、x-3 |
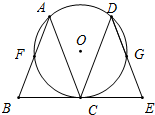 如图,在△ABC中,AB=AC,将△ABC沿BC方向平移得到△DCE,⊙O经过A、C、D三点.
如图,在△ABC中,AB=AC,将△ABC沿BC方向平移得到△DCE,⊙O经过A、C、D三点. 已知:B是线段AC上一点.且AB:BC=10:7.又D是线段AC延长线上一点.且BD:AC=11:17.若CD=16.求AB、BC的长.
已知:B是线段AC上一点.且AB:BC=10:7.又D是线段AC延长线上一点.且BD:AC=11:17.若CD=16.求AB、BC的长. 如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).
如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).