题目内容
11.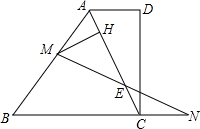 如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.
如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.
分析 过点M作BC的平行线交AC于点F,由于AB=BC,MF∥BC,得到AM=FM,因为MH⊥AC,H是AF的中点,再证△MFE≌△NCE,得到FE=EC,所以E是FC的中点,
所以EH=$\frac{1}{2}$AC,即可解答.
解答 解:过点M作BC的平行线交AC于点F,
∵AB=BC,
∴∠BAC=∠BCA,
∵MF∥BC,
∴∠AFM=∠ACB,
∴∠AFM=∠BAC,
∴AM=FM,
∵MH⊥AC,
∴H是AF的中点,
∵AM=CN,
∴FM=CN,
∵MF∥BC,
∴∠FME=∠N,
在△MFE和△NCE中,
$\left\{\begin{array}{l}{∠FME=∠N}\\{∠MEF=∠NEC}\\{MF=CF}\end{array}\right.$,
∴△MFE≌△NCE,
∴FE=EC,
∴E是FC的中点,
∴HE=HF+EF=$\frac{1}{2}$AF+$+\frac{1}{2}$FC=$\frac{1}{2}$(AF+FC)=$\frac{1}{2}$AC,
在Rt△ADC中,AC=$\sqrt{A{D}^{2}+C{D}^{2}}=\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,
∴HE=$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是作辅助线,过点M作BC的平行线交AC于点F,得到H是AF的中点,E是FC的中点.

练习册系列答案
相关题目
16.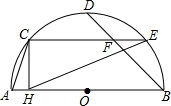 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
20.如图是一个简单的数值运算程序,当输入的x的值为-1时,则输出的值为( )


| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
1.点A(3,-4)关于原点的对称点为( )
| A. | (3,4) | B. | (-3,4) | C. | (-3,-4) | D. | (4,3) |
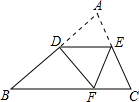 如图,D是AB边上的中点,DE∥BC,将△ABC沿过D的直线折叠,使点A落在BC上F处,
如图,D是AB边上的中点,DE∥BC,将△ABC沿过D的直线折叠,使点A落在BC上F处,