题目内容
16.已知x1,x2是方程x2-(2k+1)+(k2+1)=0的两个实数根,且x12+x22=5,则k=1.分析 由根与系数的关系可得:x1+x2=2k+1,x1•x2=k2+1,又知x12+x22=5,据此可以求得k的值.
解答 解:由根与系数的关系可得:
x1+x2=2k+1,x1•x2=k2+1,
又知x12+x22=(x1+x2)2-2x1•x2=(2k+1)2-2(k2+1)=5,
解得:k=-3,或k=1,
∵△=b2-4ac=(2k+1)2-4(k2+1)=4k-3≥0,
∴k>$\frac{3}{4}$,
∴k=1.
故答案为:1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系,根的判别式,知道△≥0是解题的关键.

练习册系列答案
相关题目
7.在下列各轴对称图案中,对称轴条数相同的是( )


| A. | (1)和(3) | B. | (2)和(4) | C. | (1)、(2)和(3) | D. | (1)、(2)和(4) |
5.实数-2,0.33,$\frac{1}{7}$,-π,$\sqrt{2}$中,无理数出现的频率是( )
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
6.某小区2门六户一个月使用的煤气的费用如表所示:
那么这六户人家使用煤气的费用的众数和中位数分别是32、31.
| 门牌号 | 101 | 102 | 201 | 202 | 301 | 302 |
| 煤气费用(元) | 25 | 18 | 32 | 40 | 30 | 32 |
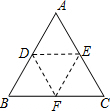 如图,折叠一张等边三角形纸片ABC,使点A落在BC边上的点,且折痕DE∥BC,问:△DBF和△EFC是不是等边三角形?请说明理由.
如图,折叠一张等边三角形纸片ABC,使点A落在BC边上的点,且折痕DE∥BC,问:△DBF和△EFC是不是等边三角形?请说明理由.