题目内容
3.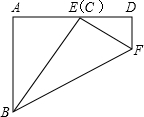 在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
分析 先由翻折变换以及矩形的性质得出∠BCF=90°,AD=BC,再根据平角的定义求出∠ACB=50°,然后在Rt△ABC中,利用正弦函数的定义得到BC=$\frac{AB}{sin50°}$≈3.9.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠BCF=90°,AD=BC.
∵∠DEF=40°,
∴∠ACB=50°.
∵在Rt△ABC中,sin∠ACB=$\frac{AB}{BC}$,
∴BC=$\frac{AB}{sin50°}$≈$\frac{3}{0.76}$≈3.9.
答:矩形的长AD约为3.9.
点评 本题考查了解直角三角形的应用,翻折变换的性质,矩形的性质,平角的定义,锐角三角函数的定义,得出AD=BC,∠ACB=50°是解题的关键.

练习册系列答案
相关题目
15.若x1、x2是一元二次方程(x-3)(x-4)=2的两个解,则|x1-x2|的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.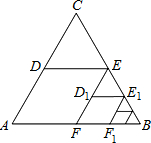 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2;…;照此规律作下去,则S5为( )
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2;…;照此规律作下去,则S5为( )
 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2;…;照此规律作下去,则S5为( )
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2;…;照此规律作下去,则S5为( )| A. | $\frac{\sqrt{3}}{8}$×($\frac{1}{4}$)4 | B. | $\frac{\sqrt{3}}{4}$×($\frac{1}{4}$)4 | C. | $\frac{\sqrt{3}}{8}$×($\frac{1}{4}$)5 | D. | $\frac{\sqrt{3}}{4}$×($\frac{1}{4}$)5 |