题目内容
19.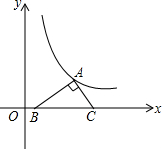 如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.
如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.
分析 因为点A在反比例函数的图象上,且Rt△ABC中,∠A=90°,∠B=60°,AB=1,能求出点A的纵坐标,进而求出横坐标到点C的长,从而能求出C的坐标.
解答  解:作AD⊥BC于D点.
解:作AD⊥BC于D点.
∵∠A=90°,∠B=60°,AB=1,
∴AD=$\frac{1}{2}$,BC=$\frac{2\sqrt{3}}{3}$,BD=$\frac{\sqrt{3}}{2}$.
∵A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,
∴A的横坐标为2$\sqrt{3}$,
∴当C点在D点的左侧时,其横坐标为:$\frac{2\sqrt{3}}{3}$+(2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$)=$\frac{13\sqrt{3}}{6}$.
当C点在D点的右侧时,其横坐标为:2$\sqrt{3}$-($\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{3}}{2}$)=$\frac{11\sqrt{3}}{6}$.
故答案为:($\frac{13\sqrt{3}}{6}$,0)或($\frac{11\sqrt{3}}{6}$,0).
点评 本题考查反比例函数的综合题,关键知道直角三角形中30°角所对的边和斜边的关系,以及反比例函数知道纵坐标求横坐标的知识点.

练习册系列答案
相关题目
7.在下列各轴对称图案中,对称轴条数相同的是( )


| A. | (1)和(3) | B. | (2)和(4) | C. | (1)、(2)和(3) | D. | (1)、(2)和(4) |
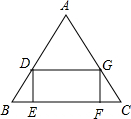 如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;
如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;