题目内容
19.把下列各式分解因式.(1)x2y-4y
(2)x2(y-3x)2-y2(3x-y)2
(3)x3-x2y-xy2+y3
(4)x(x-1)+y(y-1)+2xy
(5)x2-5x+6
(6)n2+n-20
(7)x2-9y2+x+3y
(8)x4-x3+3x-3.
分析 (1)原式提取公因式,再利用平方差公式分解即可;
(2)原式变形后,提取公因式,再利用平方差公式分解即可;
(3)原式结合后,提取公因式,再利用平方差公式分解即可;
(4)原式整理分组后,提取公因式即可得到结果;
(5)原式利用十字相乘法分解即可;
(6)原式利用十字相乘法分解即可;
(7)原式分组结合后,利用平方差公式及提取公因式即可得到结果;
(8)原式分组结合后,提取公因式即可得到结果.
解答 解:(1)x2y-4y=y(x2-4)=y(x+2)(x-2);
(2)x2(y-3x)2-y2(3x-y)2=(3x-y)2(x2-y2)=(3x-y)2(x+y)(x-y);
(3)x3-x2y-xy2+y3=x2(x-y)-y2(x-y)=(x-y)(x2-y2)=(x-y)2(x+y);
(4)x(x-1)+y(y-1)+2xy=x2+y2+2xy-(x+y)=(x+y)2-(x+y)=(x+y)(x+y-1);
(5)x2-5x+6=(x-2)(x-3);
(6)n2+n-20=(n-4)(n+5);
(7)x2-9y2+x+3y=(x+3y)(x-3y)+(x+3y)=(x+3y)(x-3y+1);
(8)x4-x3+3x-3=x3(x-1)+3(x-1)=(x-1)(x3+3).
点评 此题考查了提公因式法与公式法的综合运用,以及分组分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
 有一张纸片的形状如图所示,其中已知∠1=∠2,纸片中的△ABC和△ADC是全等的,小红说:“只要给我一个量角器,我就能验证:这两个三角形是全等.”小明不相信,你知道小红是怎样做的吗?如果知道,请写出小红的验证过程.
有一张纸片的形状如图所示,其中已知∠1=∠2,纸片中的△ABC和△ADC是全等的,小红说:“只要给我一个量角器,我就能验证:这两个三角形是全等.”小明不相信,你知道小红是怎样做的吗?如果知道,请写出小红的验证过程.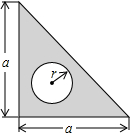 一块三角尺的形状和尺寸如图所示,如果圆孔的半径是r,三角尺的厚度是h,用式子表示这块三角尺的体积V,若a=6cm,r=0.5cm,h=0.2cm,求V的值(π取3).
一块三角尺的形状和尺寸如图所示,如果圆孔的半径是r,三角尺的厚度是h,用式子表示这块三角尺的体积V,若a=6cm,r=0.5cm,h=0.2cm,求V的值(π取3).