题目内容
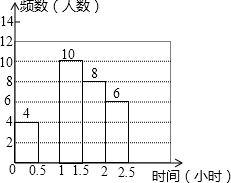 兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.| 时间(小时) | 频数(人数) | 频率 |
| 0≤t<0.5 | 4 | 0.1 |
| 0.5≤t<1 | a | 0.3 |
| 1≤t<1.5 | 10 | 0.25 |
| 1.5≤t<2 | 8 | b |
| 2≤t<2.5 | 6 | 0.15 |
| 合计 | 1 |
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
考点:频数(率)分布直方图,用样本估计总体,频数(率)分布表
专题:图表型
分析:(1)根据每天完成家庭作业的时间在0≤t<0.5的频数和频率,求出抽查的总人数,再用总人数乘以每天完成家庭作业的时间在0.5≤t<1的频率,求出a,再用每天完成家庭作业的时间在1.5≤t<2的频率乘以总人数,求出b即可;
(2)根据(1)求出a的值,可直接补全统计图;
(3)用每天完成家庭作业时间在1.5小时以内的人数所占的百分比乘以该校的总人数,即可得出答案.
(2)根据(1)求出a的值,可直接补全统计图;
(3)用每天完成家庭作业时间在1.5小时以内的人数所占的百分比乘以该校的总人数,即可得出答案.
解答:解:(1)抽查的总的人数是:
=40(人),
a=40×0.3=12(人),
b=
=0.2;
故答案为:12,0.2;
(2)根据(1)可得:每天完成家庭作业的时间在0.5≤t<1的人数是12,补图如下:

(3)根据题意得:
×1400=910(名),
答:约有多少910名学生在1.5小时以内完成了家庭作业.
| 4 |
| 0.1 |
a=40×0.3=12(人),
b=
| 8 |
| 40 |
故答案为:12,0.2;
(2)根据(1)可得:每天完成家庭作业的时间在0.5≤t<1的人数是12,补图如下:

(3)根据题意得:
| 4+12+10 |
| 40 |
答:约有多少910名学生在1.5小时以内完成了家庭作业.
点评:本题考查了频数(率)分布直方图、频数(率)分布表以及用样本估计总体,在读频数分布直方图时和利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成).
为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成).
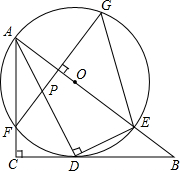 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.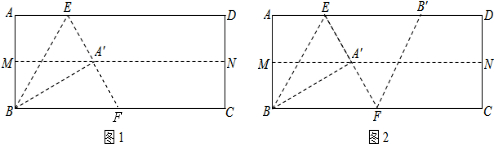
 如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为
如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为