题目内容
15. 如图,△ABC的两条高BD,CE交于点F,延长CE到Q,使CQ=AB,在BD上截取BP=AC,连接AP.
如图,△ABC的两条高BD,CE交于点F,延长CE到Q,使CQ=AB,在BD上截取BP=AC,连接AP.求证:(1)AQ=AP;(2)AQ⊥AP.
分析 (1)根据垂直的定义得到∠ADB=∠AEC=90°,得到∠ABD=∠ACQ=90°-∠BAC.推出△APB≌△QAC(SAS),根据全等三角形的性质即可得到结论;
(2)通过△APB≌△QAC,得∠BAP=∠CQA,通过等量代换得∠BAP+∠QAE=90°即可得AP⊥AQ.
解答 证明:(1)∵CF⊥AB,BE⊥AC,
∴∠ADB=∠AEC=90°,
∴∠ABD=∠ACQ=90°-∠BAC.
∵BP=AC,CQ=AB,
在△APB和△QAC中,
$\left\{\begin{array}{l}{BP=AC}\\{∠ABD=∠ACQ}\\{CQ=AB}\end{array}\right.$,
∴△APB≌△QAC(SAS),
∴AP=AQ,
(2)∵△APB≌△QAC,
∴∠BAP=∠CQA,
∵∠CQA+∠QAE=90°,
∴∠BAP+∠QAE=90°.
即AP⊥AQ.
点评 本题考查了全等三角形的性质和判定,垂直定义,三角形内角和定理的应用,解此题的关键是推出△APB≌△QAC,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
2.已知∠A为锐角,tan(75°-A)=1,则∠A的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |

 如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:
如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式: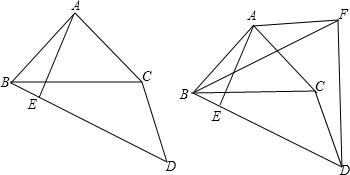
 如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,则BH和AC的大小关系如何?并说明理由.猜想:若∠ABC=135°,其他条件不变,则BH和AC的大小关系将发生什么变化?
如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,则BH和AC的大小关系如何?并说明理由.猜想:若∠ABC=135°,其他条件不变,则BH和AC的大小关系将发生什么变化?