题目内容
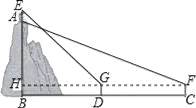
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(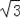 取1.732,结果保留整数)
取1.732,结果保留整数)
 411米.
【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造边角关系,进而可求出答案.
试题解析:设AH=x米,在Rt△EHG中,∵∠EGH=45°,∴GH=EH=AE+AH=x+12,∵GF=CD=288米,∴HF=GH+GF=x+12+288=x+300,在Rt△AHF中,∵∠AFH=30°,∴AH=HF•tan∠AFH,即x=(x...
411米.
【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造边角关系,进而可求出答案.
试题解析:设AH=x米,在Rt△EHG中,∵∠EGH=45°,∴GH=EH=AE+AH=x+12,∵GF=CD=288米,∴HF=GH+GF=x+12+288=x+300,在Rt△AHF中,∵∠AFH=30°,∴AH=HF•tan∠AFH,即x=(x...
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
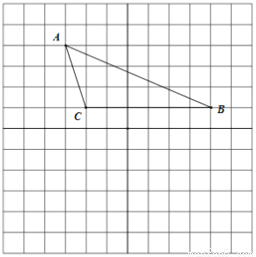
小学生10分钟应用题系列答案如图,将三角形ABC放在12*12的正方形网格中,每个小正方形的边长均为1,点A,B,C在格点上
(1)三角形ABC的面积是
(2)画出以点C为旋转中心,将三角形ABC按顺时针方向旋转90度后的三角形A’B’C’
 (1)9;(2)见解析.
【解析】试题分析:(1)由图可知BC=6,BC边上的高为3,根据三角形的面积公式即可得出结果;
(2)根据旋转的性质,分别画出A点和B点的对应点A’、B’,然后连接A’C,A’B’,B’C即可.
试题解析:
(1)由图可知BC=6,BC边上的高为3,
所以三角形ABC的面积是×6×3=9;
(2)如图:
(1)9;(2)见解析.
【解析】试题分析:(1)由图可知BC=6,BC边上的高为3,根据三角形的面积公式即可得出结果;
(2)根据旋转的性质,分别画出A点和B点的对应点A’、B’,然后连接A’C,A’B’,B’C即可.
试题解析:
(1)由图可知BC=6,BC边上的高为3,
所以三角形ABC的面积是×6×3=9;
(2)如图: 若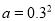 ,
, 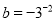 ,
, 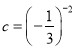 ,
, 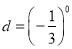 ,则( ).
,则( ).
A. 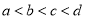 B.
B. 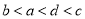 C.
C. 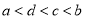 D.
D. 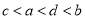
 B
【解析】试题解析:
故选B.
B
【解析】试题解析:
故选B. 在一次抽奖中,若抽中的概率是0.34,则抽不中的概率是( )
A. 0.34 B. 0.17 C. 0.66 D. 0.76
 C
【解析】在一次抽奖中,抽中的概率和抽不中的概率之和是1,抽中的概率是0.34,则抽不中的概率是1-0.34=0.66,故选C.
C
【解析】在一次抽奖中,抽中的概率和抽不中的概率之和是1,抽中的概率是0.34,则抽不中的概率是1-0.34=0.66,故选C. 一个事件的概率不可能是( )
A. 0 B. 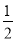 C. 1 D.
C. 1 D. 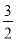
 D
【解析】一个事件的概率不可能是.
故选D.
D
【解析】一个事件的概率不可能是.
故选D. 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
 20.0米.
【解析】试题分析:此题属于实际应用问题,解题的关键是将实际问题转化为数学问题进行解答;解题时要注意构造相似三角形,利用相似三角形的性质解题.
试题解析:如图:过点D作DG⊥AB,分别交AB、EF于点G、H,∵AB∥CD,DG⊥AB,AB⊥AC,∴四边形ACDG是矩形,∴EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,∵EF∥AB,∴,由题意,知FH=EF﹣...
20.0米.
【解析】试题分析:此题属于实际应用问题,解题的关键是将实际问题转化为数学问题进行解答;解题时要注意构造相似三角形,利用相似三角形的性质解题.
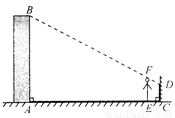
试题解析:如图:过点D作DG⊥AB,分别交AB、EF于点G、H,∵AB∥CD,DG⊥AB,AB⊥AC,∴四边形ACDG是矩形,∴EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,∵EF∥AB,∴,由题意,知FH=EF﹣... 如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB= ,则cos∠ADC= .
,则cos∠ADC= .
 【解析】试题分析:首先在△ABC中,根据三角函数值计算出AC=,再利用勾股定理计算出AD=10,然后根据余弦定义可算出cos∠ADC=.
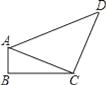
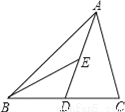
【解析】试题分析:首先在△ABC中,根据三角函数值计算出AC=,再利用勾股定理计算出AD=10,然后根据余弦定义可算出cos∠ADC=. 如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是__.
 6
【解析】试题分析:三角形的中线将三角形分成面积相等的两部分,则△ABD的面积=△ABC的面积=12,△ABE的面积=△ABD的面积=6.
6
【解析】试题分析:三角形的中线将三角形分成面积相等的两部分,则△ABD的面积=△ABC的面积=12,△ABE的面积=△ABD的面积=6. 观察如下图所示的各个图形,其中全等图形正确的是( ).
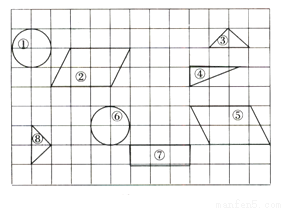
A. ②≌④ B. ⑤≌⑧ C. ①≌⑥ D. ③≌⑦
 C
【解析】观察可知 ②≌⑤,③≌⑧,①≌⑥,
故选C.
C
【解析】观察可知 ②≌⑤,③≌⑧,①≌⑥,
故选C. 
